��Ŀ����
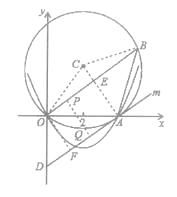
����Ŀ����ͼ��C���ڽӡ�AOB�У�AB=AO=4��tan��AOB= ![]() ��������y=ax2+bx������A��4,0����㣨-2,6��.
��������y=ax2+bx������A��4,0����㣨-2,6��.
��1���������ߵĺ�������ʽ��
��2��ֱ��m��C�����ڵ�A����y���ڵ�D����֤��AD//OB��
��3���ڣ�2���������£���P���߶�OB�ϣ��ӵ�O�������B�˶���ͬʱ����Q���߶�DA�ϣ��ӵ�D�������A�˶�����P���ٶ�Ϊÿ��1����λ������Q���ٶ�Ϊÿ��2����λ������PQ��ADʱ�����˶�ʱ��t��ֵ.
���𰸡�
��1��
�⣺��������y=ax2+bx������A��4,0����㣨-2,6����
�� ![]()
��� 
���������ߵĽ���ʽΪy= ![]() .
.
��2��
�⣺��ͼ������AC��OB�ڵ�E������OC��BC��
��OC=BC��AB=AO��
��AC��OB��
��ADΪ���ߣ�
��AC��AD��
��AD//OB.
��3��
�⣺��tan��AOB= ![]() ��
��
��sin��AOB= ![]() ��
��
��AE=OA��sin��AOB=4�� ![]() =2.4��
=2.4��
��AD//OB��
���OAD=��AOB��
��OD=OA��tan��OAD=OA��tan��AOB=4�� ![]() =3��
=3��
��PQ��ADʱ��OP=t��DQ=2t��
��O����OF��AD��F��
��Rt��ODF��OD=3��OF=AE=2.4��DF=DQ-FQ=DQ-OP=2t-t=t��
�ɹ��ɶ����ã�DF= ![]() =
= ![]() =1.8��
=1.8��
��t=1.8��.
����������1���������������뺯������ʽ�����a��b��ֵ���ɣ���2������AC��OB�ڵ�E������OC��BC������AO=AB�����ݡ������������ɵ�Aƽ�ֻ�OB����AC��OB������ADΪ���ߣ���AC��AD����AD//OB.��3��OP=t��DQ=2t���ɹ�O����OF��AD��F����DF=DQ-FQ=DQ-OP=2t-t=t������ֻҪ���DF���ɣ�����tan��AOB= ![]() ����AD//OB��AO=4�����.
����AD//OB��AO=4�����.
�����㾫����������Ŀ����֪���������ö��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�






