题目内容
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形 ![]() )靠墙摆放,高
)靠墙摆放,高 ![]() ,宽
,宽 ![]() ,小强身高
,小强身高 ![]() ,下半身
,下半身 ![]() ,洗漱时下半身与地面成
,洗漱时下半身与地面成 ![]() (
( ![]() ),身体前倾成
),身体前倾成 ![]() (
( ![]() ),脚与洗漱台距离
),脚与洗漱台距离 ![]() (点
(点 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一直线上).
在同一直线上).
(1)此时小强头部 ![]() 点与地面
点与地面 ![]() 相距多少?
相距多少?
(2)小强希望他的头部 ![]() 恰好在洗漱盆
恰好在洗漱盆 ![]() 的中点
的中点 ![]() 的正上方,他应向前或后退多少?
的正上方,他应向前或后退多少?
( ![]() ,
, ![]() ,
, ![]() ,结果精确到
,结果精确到 ![]() )
)
【答案】
(1)
解:过点F作FN⊥DK于点N,过点E作EM⊥FN于点M,
∵EF+FG=166,FG=100,∴EF=66,
∵∠FGK=80°,∴FN=100sin80°≈98,
又∵∠EFG=125°,∴∠EFM=180°-125°-10°=45°,
∴FM=66cos45°=33![]() ≈46.53,
≈46.53,
∴MN=FN+FM≈144.5.
∴他头部E点与地面DK相距约144.5cm。
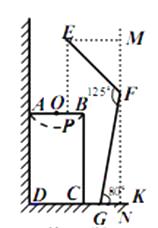
(2)
解:过点E作EP⊥AB于点P,延长OB交MN于点H。
∵AB=48,O为AB的中点,
∴AO=BO=24,
∵EM=66sin45°≈46.53,即PH≈46.53
GN=100cos80°≈1,8,CG=15,
∴OH=24+15+18==57
OP=OH-PH=57-46.53=10.47≈10.5,
∴他应向前10.5cm。

【解析】(1)过点F作FN⊥DK于点N,过点E作EM⊥FN于点M,他头部E点与地面DK的距离即为MN,由EF+FG=166,FG=100,则EF=66,由角的正弦值和余弦值即可解答;
(2)过点E作EP⊥AB于点P,延长OB交MN于点H,即求OP=OH-PH,而PH=EM,OH=OB+BH=OB+CG+GN,在Rt△EMF求出EM,在Rt△FGN求出GN即可.
【考点精析】认真审题,首先需要了解解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)).

 小题狂做系列答案
小题狂做系列答案






