题目内容
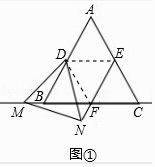
【题目】如图,等边三角形ABC中,点D、E、F、分别为边AB,AC,BC的中点,M为直线BC动点,△DMN为等边三角形
(1)如图1,当点M在点B左侧时,请你判断EN与MF有怎样的数量关系?
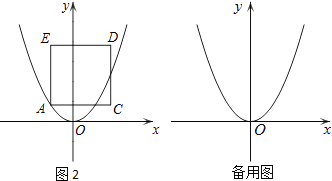
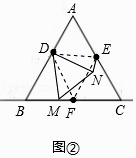
(2)如图2,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图2证明;若不成立请说明理由;
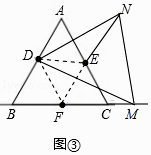
(3)若点M在点C右侧时,请你在图3中画出相应的图形,并判断(1)的结论是否仍然成立?若成立,请直接写出结论,若不成立请说明理由.
【答案】
(1)
解:EN与MF相等,
证明:连接DE、DF,
∵△ABC和△DMN为等边三角形,
∴DM=DN,∠MDN=60°,
∵点D、E、F、分别为边AB,AC,BC的中点,
∴△DEF是等边三角形,
∴∠MDF=∠NDE,
在△DMF和△DNE中,
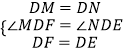 ,
,
∴△DMF≌△DNE,
∴EN=MF;
(2)
解:成立,
证明:连结DE,DF,EF.
∵△ABC是等边三角形,
∴AB=AC=BC.
∵D,E,F是三边的中点,
∴DE,DF,EF为三角形的中位线.
∴DE=DF=EF,∠FDE=60°.
又∠MDF+∠FDN=60°,∠NDE+∠FDN=60°,
∴∠MDF=∠NDE.
在△DMF和△DNE中,
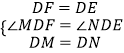 ,
,
∴△DMF≌△DNE,
∴MF=NE;
(3)
解:画出图形如图③所示:
MF与EN相等的结论仍然成立.
由(2)得,△DMF≌△DNE,
∴MF=NE.
【解析】(1)连接DE、DF,根据等边三角形的性质得到∠MDF=∠NDE,证明△DMF≌△DNE,根据全等三角形的性质证明;(2)与(1)的方法相同;(3)根据题意画出图形,证明△DMF≌△DNE,根据全等三角形的性质证明.
【考点精析】利用全等三角形的性质和等边三角形的性质对题目进行判断即可得到答案,需要熟知全等三角形的对应边相等; 全等三角形的对应角相等;等边三角形的三个角都相等并且每个角都是60°.