题目内容
【题目】直线y=﹣x﹣2与反比例函数y= ![]() 的图象交于A、B两点,且与x、y轴交于C、D两点,A点的坐标为(﹣3,k+4).
的图象交于A、B两点,且与x、y轴交于C、D两点,A点的坐标为(﹣3,k+4).
(1)求反比例函数的解析式
(2)把直线AB绕着点M(﹣1,﹣1)顺时针旋转到MN,使直线MN⊥x轴,且与反比例函数的图象交于点N,求旋转角大小及线段MN的长.
【答案】
(1)
解:将A(﹣3,k+4)代入直线y=﹣x﹣2得,k+4=﹣(﹣3)﹣2,解得k=﹣3,
∴点A坐标为(﹣3,1),
所以反比例函数的解析式为y=﹣ ![]()
(2)
解:如图,
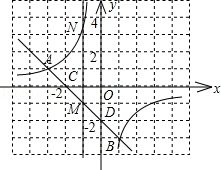
∵C、D两点的坐标为(﹣2,0)、(0,﹣2),
∴在△OCD中,∠OCD=45°;
∵直线MN⊥x轴,
∴∠CMN=45°,
∴旋转角为45°.
把x=﹣1代入y=﹣ ![]() 得,y=3,
得,y=3,
∴N的坐标为(﹣1,3),
∴MN的长度=3﹣(﹣1)=4.
【解析】(1)把A(﹣3,k+4)代入直线y=﹣x﹣2得,可得到k的值,即确定反比例函数的解析式;(2)由C、D两点的坐标得到∠OCD=45°;当直线MN⊥x轴,即可得到∠CMN=45°,得到旋转角的度数;把x=﹣1代入y=﹣ ![]() 可确定N点坐标,易得MN的长.
可确定N点坐标,易得MN的长.
【考点精析】根据题目的已知条件,利用正比例函数的图象和性质的相关知识可以得到问题的答案,需要掌握正比函数图直线,经过一定过原点.K正一三负二四,变化趋势记心间.K正左低右边高,同大同小向爬山.K负左高右边低,一大另小下山峦.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目




