题目内容
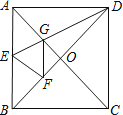
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一个含30°的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°)
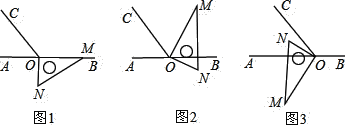
(1)将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
【答案】(1)直线ON平分∠AOC,理由详见解析;(2)t=10或t=40;(3)∠AOM–∠NOC=30°.
【解析】
(1)由角的平分线的定义和等角的余角相等求解;
(2)由∠BOC=120°可得∠AOC=60°,则∠AON=30°或∠NOR=30°,即顺时针旋转300°或120°时ON平分∠AOC,据此求解;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON、∠NOC=60°-∠AON,然后作差即可.
解:(1)直线ON平分∠AOC;
理由:
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB=60°,
又∵OM⊥ON,
∴∠MON=90°,
∴∠BON=30°,
∴∠CON=120°+30°=150°,
∴∠COD=30°,
∴OD平分∠AOC,
即直线ON平分∠AOC;
(2)由(1)可知∠BON=30°,∠DON=180°,
因此ON旋转60°或240°时直线ON平分∠AOC,
由题意得,6t=60°或240°,
∴t=10或40;
(3)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°-∠AON、∠NOC=60°-∠AON,
∴∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°.

 53随堂测系列答案
53随堂测系列答案【题目】下表为某个雨季水库管理员记录的水库一周内的水位变化情况,警戒水位为150m(上周末的水位刚好达到警戒水位).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
增减/m | +1.2 | +0.4 | +0.8 | ﹣0.1 | +0.7 | ﹣0.7 | ﹣1.1 |
注:正数表示比前一天水位上升,负数表示比前一天水位下降.
(1)本周哪一天水位最高?有多少米?
(2)本周哪一天水位最低?有多少米?
(3)根据给出的数据,以警戒水位为0点,用折线统计图表示本周内该水库的水位情况.