题目内容
【题目】已知二次函数y=ax2﹣2ax+c(a<0)的最大值为4,且抛物线过点( ![]() ,﹣
,﹣ ![]() ),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
(1)求该二次函数的解析式,及顶点D的坐标;
(2)求|PC﹣PD|的最大值及对应的点P的坐标;
(3)设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点,求t的取值.
【答案】
(1)
解:∵y=ax2﹣2ax+c的对称轴为:x=﹣ ![]() =1,
=1,
∴抛物线过(1,4)和( ![]() ,﹣
,﹣ ![]() )两点,
)两点,
代入解析式得: 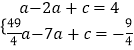 ,
,
解得:a=﹣1,c=3,
∴二次函数的解析式为:y=﹣x2+2x+3,
∴顶点D的坐标为(1,4);
(2)
解:∵C、D两点的坐标为(0,3)、(1,4);
由三角形两边之差小于第三边可知:
|PC﹣PD|≤|CD|,
∴P、C、D三点共线时|PC﹣PD|取得最大值,此时最大值为,
|CD|= ![]() ,
,
由于CD所在的直线解析式为y=x+3,
将P(t,0)代入得t=﹣3,
∴此时对应的点P为(﹣3,0)
(3)
解:y=a|x|2﹣2a|x|+c的解析式可化为:
y= ![]()
设线段PQ所在的直线解析式为y=kx+b,将P(t,0),Q(0,2t)代入得:
线段PQ所在的直线解析式:y=﹣2x+2t,
∴①当线段PQ过点(0,3),即点Q与点C重合时,线段PQ与函数
y= ![]() 有一个公共点,此时t=
有一个公共点,此时t= ![]() ,
,
当线段PQ过点(3,0),即点P与点(3,0)重合时,t=3,此时线段PQ与
y= ![]() 有两个公共点,所以当
有两个公共点,所以当 ![]() ≤t<3时,
≤t<3时,
线段PQ与y= ![]() 有一个公共点,
有一个公共点,
②将y=﹣2x+2t代入y=﹣x2+2x+3(x≥0)得:
﹣x2+2x+3=﹣2x+2t,
﹣x2+4x+3﹣2t=0,
令△=16﹣4(﹣1)(3﹣2t)=0,
t= ![]() >0,
>0,
所以当t= ![]() 时,线段PQ与y=
时,线段PQ与y= ![]() 也有一个公共点,
也有一个公共点,
③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ只与
y=﹣x2﹣2x+3(x<0)有一个公共点,此时t=﹣3,
所以当t≤﹣3时,线段PQ与y= ![]() 也有一个公共点,
也有一个公共点,
综上所述,t的取值是 ![]() ≤t<3或t=
≤t<3或t= ![]() 或t≤﹣3.
或t≤﹣3.
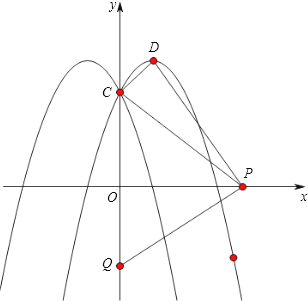
【解析】(1)先利用对称轴公式x=﹣ ![]() 计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
(2)根据三角形的三边关系:可知P、C、D三点共线时|PC﹣PD|取得最大值,求出直线CD与x轴的交点坐标,就是此时点P的坐标;
(3)先把函数中的绝对值化去,可知y= 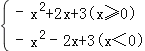 ,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数y=a|x|2﹣2a|x|+c(x≥0)时有一个公共点时,求t的值;③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ与当函数y=a|x|2﹣2a|x|+c(x<0)时也有一个公共点,则当t≤﹣3时,都满足条件;综合以上结论,得出t的取值.本题考查了二次函数的综合应用,先利用待定系数法求解析式,同时把最大值与三角形的三边关系联系在一起;同时对于二次函数利用动点求取值问题,从特殊点入手,把函数分成几部分考虑,按自变量从大到小的顺序或从小到大的顺序求解.
,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数y=a|x|2﹣2a|x|+c(x≥0)时有一个公共点时,求t的值;③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ与当函数y=a|x|2﹣2a|x|+c(x<0)时也有一个公共点,则当t≤﹣3时,都满足条件;综合以上结论,得出t的取值.本题考查了二次函数的综合应用,先利用待定系数法求解析式,同时把最大值与三角形的三边关系联系在一起;同时对于二次函数利用动点求取值问题,从特殊点入手,把函数分成几部分考虑,按自变量从大到小的顺序或从小到大的顺序求解.