题目内容
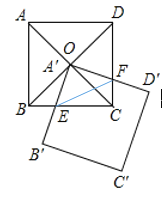
【题目】如图,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.
(1)求证:OE=OF;
(2)若正方形ABCD的边长为1,求两个正方形重叠部分的面积;
(3)若正方形 A′B′C′D′绕着O点旋转,EF的长度何时最小,并求出最小值.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用正方形的性质可得△BOE≌ △COF,即可证得OE=OF,
(2)由△BOE≌ COF,得两个正方形重叠部分的面积=S四边形ECFO=S△OEC+S△OFC= S△OEC+S△OEB=S△BOC,即可求出;
(3)利用勾股定理表示出EF的表达式,即可得到OE⊥BC时,EF最小值.
(1)在正方形ABCD中,∠OBE=∠OCF=45°,BO=CO,
又∵∠BOE+∠EOC=∠EOC+∠COF=90°,
∴∠BOE=∠COF
∴△BOE≌△COF
∴OE=OF;
(2)∵△BOE≌△COF
∴两个正方形重叠部分的面积=S四边形ECFO=S△OEC+S△OFC= S△OEC+S△OEB=S△BOC=![]() S正方形ABCD=
S正方形ABCD=![]()
(3)连接EF,∵∠EOF=90°,
∴EF2=OE2+OF2,
∵OE=OF,
∴EF2=2OE2,
∴要使EF最小,则OE最小,
∴当OE⊥BC时,OE最小=![]()
∴EF2=![]()
故EF最小值为![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目