题目内容
【题目】如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的个数是( )

①图甲,DE⊥AC,BF⊥AC ②图乙,DE平分∠ADC,BF平分∠ABC
③图丙,E是AB的中点,F是CD的中点 ④图丁,E是AB上一点,EF⊥AB.
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
①由DE⊥AC,BF⊥AC,可得DE∥BF,又由四边形ABCD是平行四边形,利用△ACD与△ACB的面积相等,即可判定DE=BF,然后由一组对边平行且相等的四边形是平行四边形,证得四边形BFDE是平行四边形;
②由四边形ABCD是平行四边形,DE平分∠ADC,BF平分∠ABC,易证得△ADE≌△CBF,则可判定DE∥BF,DE=BF,继而证得四边形BFDE是平行四边形;
③由四边形ABCD是平行四边形,E是AB的中点,F是CD的中点,易证得DF∥BE,DF=BE,继而证得四边形BFDE是平行四边形;
④无法确定DF=BE,只能证得DF∥BE,故不能判定四边形BFDE是平行四边形.
①∵四边形ABCD是平行四边形,
∴![]() ∵DE⊥AC,BF⊥AC,
∵DE⊥AC,BF⊥AC,
∴DE∥BF,![]()
∴DE=BF,
∴四边形BFDE是平行四边形;
②∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD=CB,AD∥BC,
∴∠DAE=∠BCF,
∵DE平分∠ADC,BF平分∠ABC,
∴∠ADE=∠CBF,
在△ADE和△CBF中,
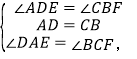
∴△ADE≌△CBF(ASA),
∴DE=BF,∠AED=∠BFC,
∴∠DEF=∠BFE,
∴DE∥BF,
∴四边形BFDE是平行四边形;
③证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB的中点,F是CD的中点,
∴![]()
∴DF=BE,
∴四边形BFDE是平行四边形;
④∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵E是AB上一点,EF⊥AB,
无法判定DF=BE,
∴四边形BFDE不一定是平行四边形。
故选:C.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案