题目内容
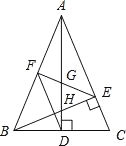
【题目】如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BCAD=
AE2；④S△ABC=4S△ADF．其中正确的有（ ）
A．1个 B．2 个 C．3 个 D．4个
【答案】D
【解析】
试题分析：由直角三角形斜边上的中线性质得出FD=
AB，证明△ABE是等腰直角三角形，得出AE=BE，证出FE=AB，延长FD=FE，①正确；证出∠ABC=∠C，得出AB=AC，由等腰三角形的性质得出BC=2CD，∠BAD=∠CAD=∠CBE，由ASA证明△AEH≌△BEC，得出AH=BC=2CD，②正确；证明△ABD～△BCE，得出
=
，即BCAD=ABBE，再由等腰直角三角形的性质和三角形的面积得出BCAD=
AE2；③正确；由F是AB的中点，BD=CD，得出S△ABC=2S△ABD=4S△ADF．④正确；即可得出结论．
练习册系列答案
相关题目
【题目】根据下表中二次函数y=ax2+bx+c（a≠0）的对应值：
x | 3.23 | 3.24 | 3.25 | 3.26 |
y | ﹣0.06 | ﹣0.02 | 0.03 | 0.09 |
判断方程ax2+bx+c=0（a≠0）的一个解x的范围是（ ）
A. 3.23＜x＜3.24 B. 3.24＜x＜3.25 C. 3.25＜x＜3.26 D. 不能确定
