Question

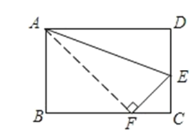
【题目】如图，四边形ABCD是一个矩形，BC=10cm，AB=8cm。现沿AE折叠，使点D恰好落在BC边上的点F处，求：（1）BF的长；（2）CE的长.

Answer 1

【答案】(1)6;(2)3.

【解析】

（1）根据折叠的性质得AF=AD=10,在直角三角形ABF利用勾股定理即可证明；（2）

由EF＝DE＝CD-CE＝8-CE，CF＝BC-BF＝4在Rt△EFC中利用EF＝CF+CE，即（8-CE）＝16+CE，即可求出CE的长.

解：∵矩形ABCD
∴AD＝BC＝10,CD＝AB＝8, ∠B＝∠C＝∠D＝90
∵△ADE沿AE折叠至△AFE
∴AF＝AD＝10,EF＝DE＝CD-CE＝8-CE
∴BF＝==6
∴CF＝BC-BF＝10-6＝4
∵EF＝CF+CE
∴（8-CE）＝16+CE
∴CE＝3