题目内容
如图,已知 ,以
,以 为直径,
为直径, 为圆心的半圆交
为圆心的半圆交 于点
于点 ,点
,点 为
为
 的中点,连接
的中点,连接 交
交 于点
于点 ,
, 为
为 的角平分线,且
的角平分线,且 ,垂足为点
,垂足为点 。
。

(1) 求证: 是半圆
是半圆 的切线;
的切线;
(2) 若 ,
, ,求
,求 的长。
的长。
 ,以
,以 为直径,
为直径, 为圆心的半圆交
为圆心的半圆交 于点
于点 ,点
,点 为
为
 的中点,连接
的中点,连接 交
交 于点
于点 ,
, 为
为 的角平分线,且
的角平分线,且 ,垂足为点
,垂足为点 。
。
(1) 求证:
 是半圆
是半圆 的切线;
的切线;(2) 若
 ,
, ,求
,求 的长。
的长。(1)证明:连接 ,
,
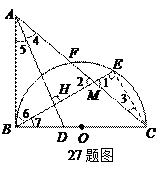

∵ 是直径, ∴
是直径, ∴ ,
,
又∵ 于
于 , ∴
, ∴ ,
,
∵ ∴
∴ 。 ······························1分
。 ······························1分
∵ 是
是 的角平分线,
的角平分线,
∴ 。 ····················…2分
。 ····················…2分
又∵ 为
为 的中点,
的中点,
∴ 。 ·····················3分
。 ·····················3分
∵ 于
于 ,
,
∵ , 即
, 即 。
。
又∵ 是直径, ∴
是直径, ∴ 是半圆
是半圆 的切线···4分
的切线···4分
(2)∵ ,
, 。
。
由(1)知, ,∴
,∴ 。·····················5分
。·····················5分
在 中,
中, 于
于 ,
, 平分
平分 ,
,
∴ ,∴
,∴ 。········································6分
。········································6分
由 ∽
∽ ,得
,得 。········································7分
。········································7分
∴ ,∴
,∴ 。················8分
。················8分
 ,
,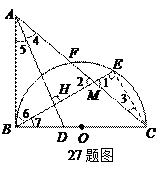

∵
 是直径, ∴
是直径, ∴ ,
,又∵
 于
于 , ∴
, ∴ ,
,∵
 ∴
∴ 。 ······························1分
。 ······························1分∵
 是
是 的角平分线,
的角平分线,∴
 。 ····················…2分
。 ····················…2分又∵
 为
为 的中点,
的中点,∴
 。 ·····················3分
。 ·····················3分∵
 于
于 ,
,∵
 , 即
, 即 。
。又∵
 是直径, ∴
是直径, ∴ 是半圆
是半圆 的切线···4分
的切线···4分(2)∵
 ,
, 。
。由(1)知,
 ,∴
,∴ 。·····················5分
。·····················5分在
 中,
中, 于
于 ,
, 平分
平分 ,
,∴
 ,∴
,∴ 。········································6分
。········································6分由
 ∽
∽ ,得
,得 。········································7分
。········································7分∴
 ,∴
,∴ 。················8分
。················8分略

练习册系列答案
相关题目