题目内容
【题目】如图所示，某办公大楼正前方有一根高度是
米的旗杆
，从办公楼顶端
测得旗杆顶端
的俯角
是
，旗杆底端
到大楼前梯坎底边的距离
是
米，梯坎坡长
是
米，梯坎坡度
，求大楼
的高度．（精确到
米，参与数据： 
， 
， 
）
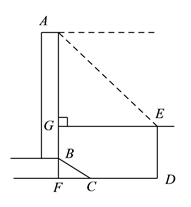
【答案】
米
【解析】延长AB交DC于H，作EG⊥AB于G，则GH=DE=15米，EG=DH，设BH=x米，则CH=
x米，在Rt△BCH中，BC=12米，由勾股定理得出方程，解方程求出BH=6米，CH=6米，得出BG、EG的长度，证明△AEG是等腰直角三角形，得出AG=EG=6
+20（米），即可得出大楼AB的高度．
解：在
中， 
，已知梯坎
的坡度
．（坡度
）∴
，由三角函数得
，
∴
．
由题意可知，四边形
为矩形．
∴
， 
．
∴
．
在等腰
中， 
．
∴
（米）．
∴大楼
的高度为
米．
练习册系列答案
相关题目
【题目】问题：探究函数y=|x|-1的性质．
小凡同学根据学习函数的经验，对函数y=|x|-1的图象与性质进行了探究．下面是小凡的探究过程，请补充完整：
（1）在函数y=|x|-1中，自变量x的取值范围是______________；
（2）下表是y与x的几组对应值．
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ||
y | 2 | 1 | 0 | -1 | 0 | 1 | m |
①m=_________；
②若A（n，9），B（10，9）为该函数图象上不同的两点，则_n=__________；
（3）如下图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；
（4）结合函数图象，解决问题：
①函数的最小值为________；
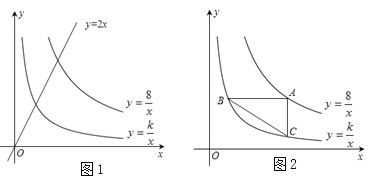
②已知直线
与函数
的图象交于C，D两点，当y1≥y时x的取值范围是___________．
