题目内容
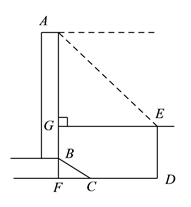
【题目】如图1,对于直线MN同侧的两个点A,B,若直线MN上的点P满足∠APM=∠BPN,则称点P为A,B在直线MN上的反射点.已知如图2,MN∥HG,AP∥BQ,点P为A,B在直线MN上的反射点,判断点B是否为P,Q在直线HG上的反射点,如果是请证明,如果不是,请说明理由.

【答案】点B是P,Q在直线HG上的反射点,理由见解析.
【解析】
依据点P为A,B在直线MN上的反射点,即可得到∠APM=∠BPQ,在根据平行线的性质,即可得到∠PBA=∠QBG,进而得出点B是P ,Q在直线HG上的反射点.
点B是P,Q在直线HG上的反射点,理由:
∵点P为A,B在直线MN上的反射点,
∴∠APM=∠BPQ,
又∵HG∥MN,
∴∠APM=∠BAP,∠BPQ=∠PBA,
∴∠PAB=∠PBA,
又∵AP∥BQ,
∴∠PAB=∠QBG,
∴∠PBA=∠QBG,
∴点B是P,Q在直线HG上的反射点.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目