题目内容
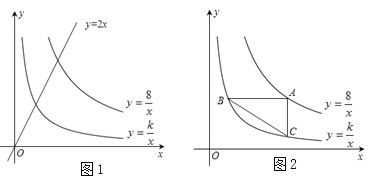
【题目】如图1，已知直线y=2x分别与双曲线
， 
交于P、Q(1，n)两点．
（1）求k的值．
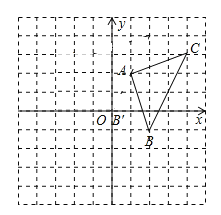
（2）如图2，点A是双曲线
上的动点，AB∥x轴，AC∥y轴，分别交双曲线
于点B、C，连接BC．试探索在点A运动过程中，△ABC的面积是否变化？若不变，请求出△ABC的面积；若改变，请说明理由；
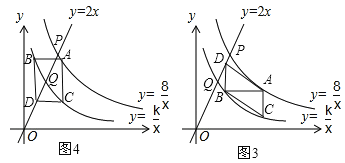
（3）如图3，过点B作AC的平行线交直线y=2x于点D，请你进一步探索在点A运动过程中，tan∠ACB=tan∠ADB能否成立？若能，求出此时点A的坐标；若不能，请说明理由．
【答案】（1）k的值为2； (2)不变；（3）能成立.当tan∠ADB= tan∠ACB时，A点的坐标为（2
， 
）或（2，4）．
【解析】试题分析：（1）将点Q（1，n）代入y=2x得求得n的值，再将点Q坐标代入
，可得k的值；
（2）设点A的坐标为（a，b），易得b=
，结合条件可用a的代数式表示点B、点C的坐标，进而表示出线段AB、AC的长，就可算出△BAC的面积是一个定值；
（3）由an∠ADB= tan∠ACB可得
，DB=AC，设出点A的坐标，则可得到相应B、D的坐标，进而表示出AC、BD，即可求得a的值.
试题解析：（1）将点Q（1，n）代入y=2x得：n=2×1=2，
将点Q（1，2）代入
得:k=2×1=2，
∴k的值为2；
（2）不变.
由题意设点A的坐标为（a， 
），
∵AB∥x轴，AC∥y轴，
∴xC=xA=a，yB=yA=b=
．
∵点B、C在双曲线y=
上，
∴xB=
=，yC=
．
∴点B的坐标为（
， 
），点C的坐标为（a， 
）．
∴AB= 
，AC=
．
∴S△ABC=
ABAC=
．
∴在点A运动过程中，△ABC的面积不变，始终等于
．
（3）能成立.
∵tan∠ADB= tan∠ACB， 
，DB=AC，
由题意设点A的坐标为（a， 
），则：
B（
， 
）、C（a， 
）、D（
， 
）
∴AC=
，DB=
∴
=
解得： 
， 
（舍），
， 
（舍）
∴点A的坐标为（2
， 
）或（2，4）．
综上所述：当tan∠ADB= tan∠ACB时，A点的坐标为（2
， 
）或（2，4
备注：当点A为（2
， 
）时，如图3所示；
当点A为（2，4）时，如图4所示.
