Question

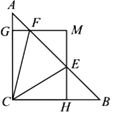
【题目】如图，AB=AE，∠B=∠E，BC=ED，点F是CD的中点，

（1）AC与AD相等吗？为什么？

（2）AF与CD的位置关系如何？说明理由；

（3）若P为AF上的一点，那么PC与PD相等吗？为什么？

Answer 1

【答案】（1）AC=AD，见解析；（2）AF⊥CD，见解析；（3）PC=PD，见解析.

【解析】

（1）由已知条件：AB=AE，∠B=∠E，BC=ED，可证得△ABC∽△AED，由此得AC=AD．
（2）由于△ACD是等腰三角形，根据等腰三角形三线合一的性质即可得到AF⊥CD．
（3）由（2）易知：AF垂直平分线段CD，即可根据线段垂直平分线的性质判定PC=PD．

（1）AC=AD.理由如下：

在△ABC与△AED中

∴△ABC≌△AED（SAS）

∴AC=AD

（2）AF⊥CD，理由如下：

∵AC=AD，点F是CD的中点

∴AF⊥CD

（3）PC=PD，理由如下：

∵点F是CD的中点，AF⊥CD

∴AF是CD的垂直平分线

∵点P在AF上

∴PC=PD