Question

【题目】在如图的正方形网格中，每一个小正方形的边长为1．格点三角形ABC（顶点是网格线交点的三角形）的顶点A、C的坐标分别是（﹣4，6），（﹣1，4）．

（1）请在图中的网格平面内建立平面直角坐标系；
（2）请画出△ABC关于x轴对称的△A1B1C1；
（3）请在y轴上求作一点P，使△PB1C的周长最小，并写出点P的坐标．

Answer 1

【答案】
（1）

解：如图所示；

（2）

解：如图，即为所求；

（3）

解：作点B关于y轴的对称点B2，连接AB2交y轴于点P，则点P即为所求．

设直线AB2的解析式为y=kx+b（k≠0），

∵A（﹣4，6），B2（2，2），

∴ ，解得 ，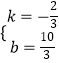

∴直线AB2的解析式为：y=﹣ x+ ，

∴当x=0时，y= ，

∴P（0， ）．

【解析】（1）根据A点坐标建立平面直角坐标系即可；（2）分别作出各点关于x轴的对称点，再顺次连接即可；（3）作出点B关于y轴的对称点B2 ， 连接B2交y轴于点P，则P点即为所求．
【考点精析】关于本题考查的勾股定理的概念和作轴对称图形，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；画对称轴图形的方法：①标出关键点②数方格，标出对称点③依次连线才能得出正确答案．