Question

【题目】在矩形纸片ABCD中，AB=6，BC=8．
（1）如图①，将矩形纸片沿AN折叠，点B落在对角线AC上的点E处，求BN的长；

（2）如图②，点M为AB上一点，将△BCM沿CM翻折至△ECM，ME与AD相交于点G，CE与AD相交于点F，且AG=GE，求BM的长；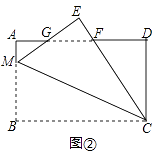

（3）如图③，将矩形纸片ABCD折叠，使顶点B落在AD边上的点E处，折痕所在直线同时经过AB、BC（包括端点），设DE=x，请直接写出x的取值范围： ．

Answer 1

【答案】
（1）

解：设BN=x，在Rt△ENC中，由勾股定理得：x2+42=（8﹣x），

解得：x=3，

∴BN=3

（2）

解：设BM=x，

由折叠的性质得：∠E=∠B=90°=∠A，

在△GAM和△GEF中， ，

∴△GAM≌△GEF（ASA），

∴GM=GF，

∴AF=ME=BM=x，EF=AM=6﹣x，

∴DF=8﹣x，CF=8﹣（6﹣x）=x+2，

在Rt△DFC中，由勾股定理得：（x+2）2=（8﹣x）2+62，

解得：x= ，

∴BM=

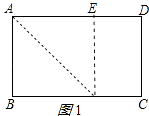
（3）解：当折痕所在直线经过点A时，如图1所示：
此时DE最小=AD﹣AB=8﹣6=2；
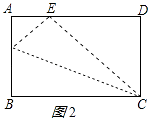
当折痕所在直线经过点C时，如图2所示：
此时DE最大，CE=CB=8，
由勾股定理得：DE= =2 ；
∴x的取值范围是2≤x≤2 ；
故答案为：2≤x≤2
【解析】（1）设BN=x，在Rt△ENC中，由勾股定理得出方程，解方程即可；（2）由ASA证明△GAM≌△GEF（ASA），得出GM=GF，AF=ME=BM=x，EF=AM=6﹣x，因此DF=8﹣x，CF=x+2，在Rt△DFC中，由勾股定理得出方程，解方程即可；（3）当折痕所在直线经过点A时，如图1所示；此时DE最小=AD﹣AB=8﹣6=2；当折痕所在直线经过点C时，如图2所示：此时DE最大，CE=CB=8，由勾股定理得：DE= =2 ；∴x的取值范围是2≤x≤2 ；所以答案是：2≤x≤2 ．
【考点精析】通过灵活运用翻折变换（折叠问题），掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等即可以解答此题．