Question

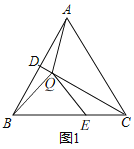
【题目】如图1，在等边△ABC中，CD为中线，点Q在线段CD上运动，将线段QA绕点Q顺时针旋转，使得点A的对应点E落在射线BC上，连接BQ，设∠DAQ=α（0°＜α＜60°且α≠30°）．
（1）当0°＜α＜30°时，
①在图1中依题意画出图形，并求∠BQE（用含α的式子表示）；
②探究线段CE，AC，CQ之间的数量关系，并加以证明；

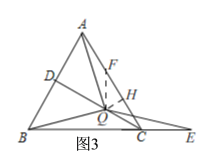
（2）当30°＜α＜60°时，直接写出线段CE，AC，CQ之间的数量关系．

Answer 1

【答案】（1）图形见解析；∠BQE=60°+2α；（2）CE+AC=CQ；证明见解析；（3）AC-CE=CQ．

【解析】

（1）①先根据等边三角形的性质的QA=QB，进而得出QB=QE，最后用三角形的内角和定理即可得出结论；
②延长CA到点F，使得AF=CE，连接QF，作QH⊥AC于点H．先判断出△QAF≌△QEC，得出QF=QC，再判断出△QCF是底角为30度的等腰三角形，再构造出直角三角形即可得出结论；
（2）同②的方法即可得出结论．

（1）当0°＜α＜30°时，
①画出的图形如图1所示，

∵△ABC为等边三角形，
∴∠ABC=60°．
∵CD为等边三角形的中线，
∴CD是AB的垂直平分线，

∵Q为线段CD上的点，
∴QA=QB．
∵∠DAQ=α，
∴∠ABQ=∠DAQ=α，∠QBE=60°-α．
∵线段QE为线段QA绕点Q顺时针旋转所得，
∴QE=QA．
∴QB=QE．
∴∠QEB=∠QBE=60°-α，
∴∠BQE=180°-2∠QBE=180°-2（60°-α）=60°+2α；
②CE+AC=CQ；证明：

如图2，延长CA到点F，使得AF=CE，连接QF，作QH⊥AC于点H．

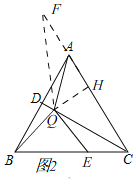
∵∠BQE=60°+2α，点E在BC上，
∴∠QEC=∠BQE+∠QBE=（60°+2α）+（60°-α）=120°+α．
∵点F在CA的延长线上，∠DAQ=α，
∴∠QAF=∠BAF+∠DAQ=120°+α．
∴∠QAF=∠QEC．
又∵AF=CE，QA=QE，
∴△QAF≌△QEC．
∴QF=QC．
∵QH⊥AC于点H，
∴FH=CH，CF=2CH．
∵在等边三角形ABC中，CD为中线，
点Q在CD上，
∴∠ACQ=∠ACB=30°，
即△QCF为底角为30°的等腰三角形．
∴CH＝CQcos∠HCQ＝CQcos30°＝CQ．
∴CE+AC=AF+AC=CF=2CH＝CQ．
（2）如图3，当30°＜α＜60°时，
在AC上取一点F使AF=CE，

∵△ABC为等边三角形，
∴∠ABC=60°．
∵CD为等边三角形的中线，
∵Q为线段CD上的点，
∴CD是AB的垂直平分线，
由等边三角形的对称性得QA=QB．
∵∠DAQ=α，
∴∠ABQ=∠DAQ=α，∠QBE=60°-α．
∵线段QE为线段QA绕点Q顺时针旋转所得，
∴QE=QA．
∴QB=QE．
∴∠QEB=∠QBE=60°-α=∠QAF，
又∵AF=CE，QA=QE，
∴△QAF≌△QEC．
∴QF=QC．
∵QH⊥AC于点H，
∴FH=CH，CF=2CH．
∵在等边三角形ABC中，CD为中线，点Q在CD上，
∴∠ACQ=∠ACB=30°，
即△QCF为底角为30°的等腰三角形．
∴CH＝CQcos∠HCQ＝CQcos30°＝CQ．
∴AC-CE=AC-AF=CF=2CH＝CQ．