题目内容
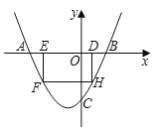
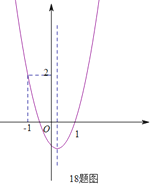
【题目】在平面直角坐标系 xOy 中，抛物线 y mx
2mx 3与 y 轴交于点C ，该抛物线对称轴与 x 轴的交于点 A．
（1）求该抛物线的对称轴及点 A 、C 的坐标；
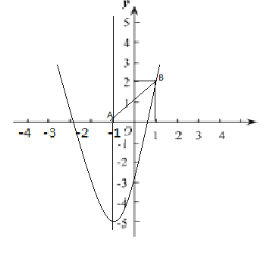
（2）点 A 向右移动两个单位长度，向上移动两个单位长度，得到点 B，若抛物线与线段 AB恰有一个交点时，结合图象，求 m 的取值范围．
【答案】（1）对称轴
，
，
（2）
或
．
【解析】
（1）由
轴上的点横坐标为0，可得C的坐标，由抛物线的对称轴公式求对称轴，再可以求A的坐标．
（2）利用函数过定点C，分
分别画出函数的大致图像，观察图像与线段AB，找到满足一个交点的条件即可得到答案．
解：（1）由抛物线的对称轴为：
，
所以对称轴为
，
令
，得
，所以抛物线与轴的交点C的坐标为（0，－3）
因为抛物线的对称轴与
轴交于点A，所以A（-1，0）
所以：抛物线的对称轴为，A（-1，0），C（0，－3）．
（2）点A（-1，0） 向右移动两个单位长度，向上移动两个单位长度，得到点 B，
所以B（1，2），因为抛物线
过C（0，-3）,
当
＞0，抛物线开口向上，把B（1，2）代入解析式得：
，
所以
，
由
越大，抛物线的开口越窄，当抛物线与线段AB恰好有一个交点时，．
当＜0，抛物线开口向下，把A（－1，0）代入解析式得：
，
所以
，
当抛物线与线段AB恰好有一个交点时，由抛物线的顶点
得；
．所以．
综上：的取值范围是或．
一线名师权威作业本系列答案
【题目】九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销售量的相关信息如下表：
时间x（天） | 1≤x＜50 | 50≤x≤90 |
售价（元/件） | x＋40 | 90 |
每天销量（件） | 200－2x | |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元[
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果.
