题目内容
【题目】如图所示，在△ABC中，∠ACB=90°，AM是BC边的中线，CN⊥AM于N点，连接BN，求证：
（1）△MCN∽△MAC；
（2）∠NBM=∠BAM.
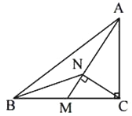
【答案】（1）见解析；（2）见解析.
【解析】
（1）根据两角对应相等的两个三角形相似，即可得出结论；
（2）由△MNC∽△MCA，得到
，再由中线的定义，得到BM=MC，即可得到
，再由两边对应成比例且夹角相等的两个三角形相似，即可得到结论．
（1）∵∠ACB=90°，CN⊥AM，∴∠ACB=∠MNC．
∵∠NMC=∠CMA，∴△MNC∽△MCA；
（2）由（1）得：△MNC∽△MCA，∴．
∵AM是BC边的中线，∴MB=MC，∴．
∵∠BMN=∠AMB，∴△MNB∽△MBA，∴∠NBM=∠BAM．
练习册系列答案
阅读快车系列答案
相关题目
