Question

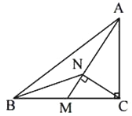
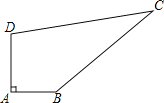
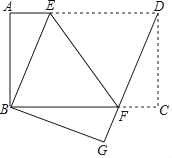
【题目】在矩形纸片ABCD中，AB=6，BC=8，现将纸片折叠，使点D与点B重合，折痕为EF，连接DF．

（1）说明△BEF是等腰三角形；

（2）求折痕EF的长．

Answer 1

【答案】（1）见解析；（2）.

【解析】

（1）根据折叠得出∠DEF=∠BEF，根据矩形的性质得出AD∥BC，求出∠DEF=∠BFE，求出∠BEF=∠BFE即可；

（2）过E作EM⊥BC于M，则四边形ABME是矩形，根据矩形的性质得出EM=AB=6，AE=BM，根据折叠得出DE=BE，根据勾股定理求出DE、在Rt△EMF中，由勾股定理求出即可．

（1）∵现将纸片折叠，使点D与点B重合，折痕为EF，∴∠DEF=∠BEF．

∵四边形ABCD是矩形，∴AD∥BC，∴∠DEF=∠BFE，∴∠BEF=∠BFE，∴BE=BF，即△BEF是等腰三角形；

（2）过E作EM⊥BC于M，则四边形ABME是矩形，所以EM=AB=6，AE=BM．

∵现将纸片折叠，使点D与点B重合，折痕为EF，∴DE=BE，DO=BO，BD⊥EF．

∵四边形ABCD是矩形，BC=8，∴AD=BC=8，∠BAD=90°．

在Rt△ABE中，AE2+AB2=BE2，即（8﹣BE）2+62=BE2，解得：BE==DE=BF，AE=8﹣DE=8﹣==BM，∴FM=﹣=．

在Rt△EMF中，由勾股定理得：EF==．

故答案为：．