题目内容
【题目】已知抛物线y=![]() x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0),B(0、﹣4)与x轴交于另一点C,连接BC.
(1)求抛物线的解析式;
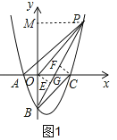
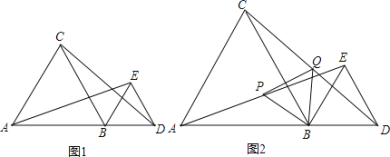
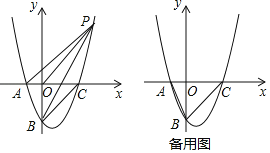
(2)如图,P是第一象限内抛物线上一点,且S△PBO=S△PBC,求证:AP∥BC;
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使△ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
【答案】(1)抛物线的解析式为:y=![]() x2﹣x﹣4;(2)证明见解析;(3)点D的坐标为(
x2﹣x﹣4;(2)证明见解析;(3)点D的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
【解析】(1)利用待定系数法求抛物线的解析式即可
(2)令y=0求抛物线与x轴的交点C的坐标,作△POB和△PBC的高线,根据面积相等可得OE=CF,证明△OEG≌△CFG,则OG=CG=2,根据三角函数列式可得P的坐标,利用待定系数法求一次函数AP和BC的解析式,k相等则两直线平行;
(3)先利用概率的知识分析A,B,C,E中的三点为顶点的三角形,有两个三角形与△ABE有可能相似,即△ABC和△BCE,
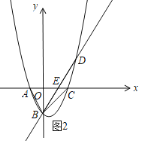
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,根据存在公共角∠BAE=∠BAC,可得△ABE∽△ACB,列比例式可得E的坐标,利用待定系数法求直线BE的解析式,与抛物线列方程组可得交点D的坐标;
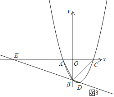
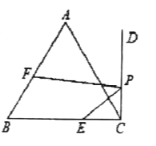
②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,同理可得结论.
(1)把点A(﹣2,0),B(0、﹣4)代入抛物线y=![]() x2+bx+c中得:
x2+bx+c中得:
![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为:y=![]() x2﹣x﹣4;
x2﹣x﹣4;
(2)当y=0时,![]() x2﹣x﹣4=0,
x2﹣x﹣4=0,
解得:x=﹣2或4,
∴C(4,0),
如图1,过O作OE⊥BP于E,过C作CF⊥BP于F,设PB交x轴于G,
∵S△PBO=S△PBC,
∴![]() PBOE=
PBOE=![]() PBCF,
PBCF,
∴OE=CF,
易得△OEG≌△CFG,
∴OG=CG=2,
设P(x,![]() x2﹣x﹣4),过P作PM⊥y轴于M,
x2﹣x﹣4),过P作PM⊥y轴于M,
tan∠PBM=![]() ,
,
∴BM=2PM,
∴4+![]() x2﹣x﹣4=2x,
x2﹣x﹣4=2x,
x2﹣6x=0,
x1=0(舍),x2=6,
∴P(6,8),
易得AP的解析式为:y=x+2,
BC的解析式为:y=x﹣4,
∴AP∥BC;
(3)以A,B,C,E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE,四种,其中△ABE重合,不符合条件,△ACE不能构成三角形,
∴当△ABE与以A,B,C,E中的三点为顶点的三角形相似,存在两个三角形:△ABC和△BC,
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,
∵∠BAE=∠BAC,∠ABE≠∠ABC,
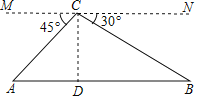
∴∠ABE=∠ACB=45°,
∴△ABE∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴AE=![]() ,
,
∴E(![]() ,0),
,0),
∵B(0,﹣4),
易得BE:y=![]() ,
,
则![]() x2﹣x﹣4=
x2﹣x﹣4=![]() x﹣4,
x﹣4,
x1=0(舍),x2=![]() ,
,
∴D(![]() ,
,![]() );
);
②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,
∵∠BEA=∠BEC,
∴当∠ABE=∠BCE时,△ABE∽△BCE,
∴![]() ,
,
设BE=2![]() m,CE=4
m,CE=4![]() m,
m,
Rt△BOE中,由勾股定理得:BE2=OE2+OB2,
∴![]() ,
,
3m2﹣8![]() m+8=0,
m+8=0,
(m﹣2![]() )(3m﹣2
)(3m﹣2![]() )=0,
)=0,
m1=2![]() ,m2=
,m2=![]() ,
,
∴OE=4![]() m﹣4=12或
m﹣4=12或![]() ,
,
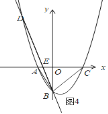
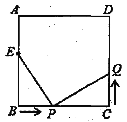
∵OE=![]() <2,∠AEB是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,如图4,
<2,∠AEB是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,如图4,
∴E(﹣12,0);
同理得BE的解析式为:y=﹣![]() x﹣4,
x﹣4,
﹣![]() x﹣4=
x﹣4=![]() x2﹣x﹣4,
x2﹣x﹣4,
x=![]() 或0(舍)
或0(舍)
∴D(![]() ,﹣
,﹣![]() );
);
综上,点D的坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).