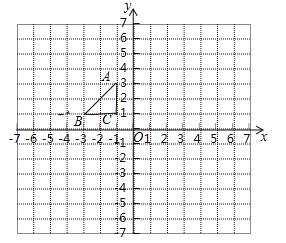题目内容
【题目】如图①,直线PQ同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点T为M,N在直线PQ上的投射点.
(1)如图②,在Rt△ABC中,∠B=60°,D为斜边AB的中点,E为AC的中点.求证:点D为C,E在直线AB上的投射点;
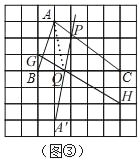
(2)如图③,在正方形网格中,已知点A,B,C三点均在格点上,请仅用没有刻度的直尺在AC上画出点P,在BC上画出点Q,使A,P在BC上的投射点Q满足CQ=2BQ;
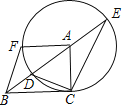
(3)如图④,在Rt△ABC中,∠C=90°,AC=BC,在AB,BC边上是否分别存在点D,E,使点D为E,C在AB上的投射点,点E为A,D在BC上的投射点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
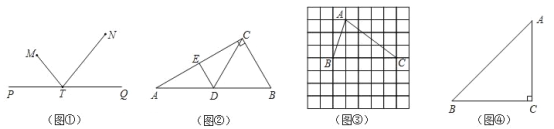
【答案】(1)证明见解析;(2)画图见解析;(3)存在,![]() .
.
【解析】
(1)先求出∠BDC=60°,进而判断出∠ADE=∠B=60°,即可得出结论;
(2)根据对称性即可作出图形;
(3)根据对称和相似作出图形,再用相似三角形的性质即可得出结论.
(1)∵在Rt△ABC中,D为斜边AB的中点,
∴CD=BD=![]() BC,
BC,
又∵∠B=60°,
∴∠BDC=60°,
∵D,E分别为AB,AC的中点,
∴DE∥AC,
∴∠ADE=∠B=60°,
∴∠ADE=∠BDC,
∴点D为C,E在直线AB上的投射点;
(2)如图③,
作法:
1、在格点上取点G,H,连接HG交BC于Q,(理由:△BQG∽△HQC)
2、作点A关于BC的对称点A',连接A'Q并延长交AC于P,(∠AQB=∠A'QB=∠PQC)
即:点P就是所求作的点;
(3)存在,
如图④,作点C关于AB的对称点C′,连接BC',AC',
则四边形ACBC′为正方形,
作点A关于BC的对称点A′,连接A'C'交AB于D,交BC于E,
即:点D,E是所求作的点,
∴C′,D,E,A在同一直线上,
CA′=CA=C′A=C′B=BC,CD=C′D,
∴△C′BE≌△A′CE,
∴BE=![]() BC=
BC=![]() C′A,
C′A,
∵AC′∥BC,
∴△BDE∽△ADC′,
∴![]() ,
,
∴![]() .
.