题目内容
【题目】一次函数y=kx+b的图象与x、y轴分别交于点A（2，0），B（0，4）．
（1）求该函数的解析式；
（2）O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC+PD的最小值，并求取得最小值时P点的坐标．
【答案】
（1）
解：将点A、B的坐标代入y=kx+b得：
0=2k+b，4=b，
∴k=﹣2，b=4，
∴解析式为：y=﹣2x+4
（2）
解：
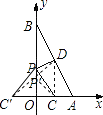
设点C关于点O的对称点为C′，连接C′D交OB于P′，连接P′C，则PC=PC′，
∴PC+PD=PC′+PD=C′D，即PC+PD的最小值是C′D．
连接CD，在Rt△DCC′中，C′D= 
=2 
，即PC′+PD的最小值为2 ，
∵OA、AB的中点分别为C、D，
∴CD是△OBA的中位线，
∴OP∥CD，CD= 
OB=2，
∵C′O=OC，
∴OP是△C′CD的中位线，
∴OP= CD=1，
∴点P的坐标为（0，1）．
【解析】（1）将点A、B的坐标代入y=kx+b并计算得k=﹣2，b=4．求出解析式为：y=﹣2x+4；（2）设点C关于点O的对称点为C′，连接C′D交OB于P，则PC=PC′，PC+PD=PC′+PD=C′D，即PC+PD的最小值是C′D．连接CD，在Rt△DCC′中，由勾股定理求得C′D的值，由OP是△C′CD的中位线而求得点P的坐标．
【考点精析】本题主要考查了一次函数的性质的相关知识点，需要掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小才能正确解答此题．
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》，这是中国足球历史上的重大改革．为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表：
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息，解答下列问题：
（1）a= ， b= ，
（2）补全频数分布直方图；
（3）若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？
（4）在这次竞赛中，甲、乙、丙、丁四位同学都获得一等奖，若从这四位同学中随机选取两位同学代表我市参加上一级竞赛，请用树状图或列表的方法，计算恰好选中甲、乙二人的概率．
