��Ŀ����
����Ŀ������Ժ�칫��2015��3��16�շ����ˡ��й�����ĸ�����巽�����������й�������ʷ�ϵ��ش�ĸΪ�˽�һ���ռ�����֪ʶ�����������Ļ������о����ˡ������У��֪ʶ�������Ϊ�˽�����֪ʶ���ռ�����������ȡ�˲��ֻ���������������õ����в�������ͳ��ͼ����
�ȴ� | Ƶ�� | Ƶ�� |
һ�Ƚ� | 10 | 0.05 |
���Ƚ� | 20 | 0.10 |
���Ƚ� | 30 | b |
��ʤ�� | a | 0.30 |
������ | 80 | 0.40 |
�����������Ϣ������������⣺
��1��a= �� b= ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����������ͳ��ͼ�������ֲ�������ʻ����ʤ����Ӧ������Բ�ĽǵĶ����Ƕ��٣�
��4������ξ����У��ס��ҡ���������λͬѧ�����һ�Ƚ�����������λͬѧ�����ѡȡ��λͬѧ�������вμ���һ��������������״ͼ���б��ķ���������ǡ��ѡ�мס��Ҷ��˵ĸ��ʣ�
���𰸡�
��1��60��0.15
��2��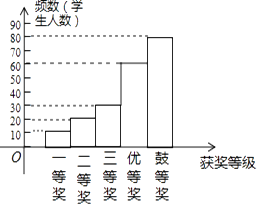
��3���⣺��ʤ���������ε�Բ�Ľ�Ϊ0.30��360��=108��
��4���⣺�б������ұ����ֱ���ABCD��ʾ��
A | B | C | D | |
A | AB | AC | AD | |
B | BA | BC | BD | |
C | CA | CB | CD | |
D | DA | DB | DC |
�߹���12�ֵȿ��ܵĽ����ǡ��ѡ��A��B����2�֣�
����״ͼ���£�
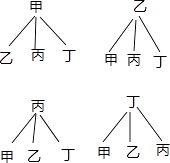
��P��ѡ��A��B��= ![]() =
= ![]() ��
��
���������⣺��1����������Ϊ10��0.05=200�ˣ� a=200��10��20��30��80=60�ˣ�
b=30��200=0.15��
�ʴ�Ϊ60��0.15��
��1�����ݹ�ʽƵ��=Ƶ����������������������������ٸ��ݹ�ʽ�ó�a��b��ֵ���ɣ���3�����ݹ�ʽ��ʤ����Ӧ������Բ�ĽǵĶ���=��ʤ����Ƶ�ʡ�360����㼴�ɣ���4������״ͼ���б������еȿ��ܵĽ���оٳ��������ø��ʹ�ʽ��⼴�ɣ�

����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ������W��x֮��ĺ�������ʽ������=���멁�ɱ�����
��3����˵����2����������W���ۼ�x�ı仯���仯���������ָ���ۼ�Ϊ����Ԫʱ������������������Ƕ��٣�
����Ŀ��С��������ķ����������2 ![]() ��3=0�Ľ⣬����������ķ���������������������̵Ľ⣬������Ľ�������д������ı����У�
��3=0�Ľ⣬����������ķ���������������������̵Ľ⣬������Ľ�������д������ı����У�
���� | ��Ԫ�����·��� | ���·��� | ���� | ��ԭ���̵Ľ� |
2 | �� | t= | t= |
|
x��2 | ||||
x+2+ |





