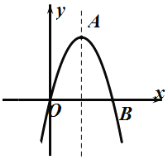Question

【题目】二次函数（，是常数）中，自变量与函数的对应值如下表：

	-1		0		1		2		3
			1		2		1		-2

（1）判断二次函数图象的开口方向，并写出它的顶点坐标；

（2）一元二次方程（，是常数）的两个根，的取值范围是下列选项中的哪一个 .

A． B．

C. D．

Answer 1

【答案】（1）抛物线的开口向下，顶点坐标为；（2）C.

【解析】

（1）观察表格，当自变量x的值逐渐增大时，函数y的值由小到大，再由大到小，即可得出函数图象的开口方向；利用二次函数的对称性即可得出顶点坐标；

（2）由函数y=ax2+bx+c的图象与x轴的交点的横坐标就是方程ax2+bx+c=0的根，根据函数的增减性即可判断方程ax2+bx+c=0两个根的范围．

解：（1）∵当x＞1时，y随x的增大而减小，x＜1时，y随x的增大而增大，

∴二次函数图象的开口向下；

∵自变量x与函数y的对应值表中，当x=1时，y的值从2开始向两边对称，

∴此函数的对称轴为：x=1，顶点坐标为：（1，2）；

（2）一元二次方程ax2+bx+c=0（a≠0，a，b，c是常数）的两个根是x1，x2，

由表格可知＜y=0＜1时＜x＜0或2＜x＜，

∴一元二次方程ax2+bx+c=0（a≠0，a，b，c是常数）的两个根x1，x2的取值范围为：＜x1＜0；2＜x2＜，

故答案为：C．