题目内容
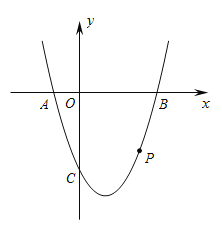
【题目】如图,抛物线![]() 与x轴相交于
与x轴相交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() .
.![]() 为抛物线上一点,横坐标为
为抛物线上一点,横坐标为![]() ,且
,且![]() .
.
⑴求此抛物线的解析式;
⑵当点![]() 位于
位于![]() 轴下方时,求
轴下方时,求![]() 面积的最大值;
面积的最大值;
⑶设此抛物线在点![]() 与点
与点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )最高点与最低点的纵坐标之差为
)最高点与最低点的纵坐标之差为![]() .
.
①求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 时,直接写出
时,直接写出![]() 的面积.
的面积.
【答案】(1)![]() ;(2)8;(3)①
;(2)8;(3)①![]() (
(![]() ),
),![]() (
(![]() ),
),![]() (
(![]() );②6.
);②6.
【解析】
(1)将点C(0,-3)代入y=(x-1)2+k即可;
(2)易求A(-1,0),B(3,0),抛物线顶点为(1,-4),当P位于抛物线顶点时,△ABP的面积有最大值;
(3)①当0<m≤1时,h=-3-(m2-2m-3)=-m2+2m;当1<m≤2时,h=-1-(-4)=1;当m>2时,h=m2-2m-3-(-4)=m2-2m+1;
②当h=9时若-m2+2m=9,此时△<0,m无解;若m2-2m+1=9,则m=4,则P(4,5),△BCP的面积=![]() (4+1)×3=6;
(4+1)×3=6;
解:(1)因为抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
把![]() 代入
代入![]() ,得
,得
![]() ,
,
解得![]() ,
,
所以此抛物线的解析式为![]() ,
,
即![]() ;
;
(2)令![]() ,得
,得![]() ,
,
解得![]() ,
,
所以![]() ,
,
所以![]() ;
;
解法一:
由(1)知,抛物线顶点坐标为![]() ,
,
由题意,当点![]() 位于抛物线顶点时,
位于抛物线顶点时,![]() 的面积有最大值,
的面积有最大值,
最大值为![]() ;
;
解法二
由题意,得![]() ,
,
所以![]()
![]()
![]() ,
,
所以当![]() 时,
时,![]() 有最大值8;
有最大值8;
(3)①当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
②当h=9时
若-m2+2m=9,此时△<0,m无解;
若m2-2m+1=9,则m=4,
∴P(4,5),
∵B(3,0),C(0,-3),
∴△BCP的面积=![]() (4+1)×3=6;
(4+1)×3=6;

 名校课堂系列答案
名校课堂系列答案【题目】二次函数![]() (
(![]() ,
,![]() 是常数)中,自变量
是常数)中,自变量![]() 与函数
与函数![]() 的对应值如下表:
的对应值如下表:
| -1 |
| 0 |
| 1 |
| 2 |
| 3 |
|
|
| 1 |
| 2 |
| 1 |
| -2 |
(1)判断二次函数图象的开口方向,并写出它的顶点坐标;
(2)一元二次方程![]() (
(![]() ,
,![]() 是常数)的两个根
是常数)的两个根![]() ,
,![]() 的取值范围是下列选项中的哪一个 .
的取值范围是下列选项中的哪一个 .
A.![]() B.
B.![]()
C. ![]() D.
D.![]()