题目内容
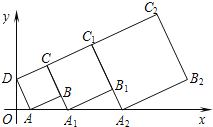
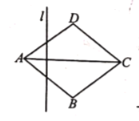
【题目】已知:如图,菱形![]() 的周长为
的周长为![]() ,对角线
,对角线![]() ,直线
,直线![]() 从点
从点![]() 出发,以1
出发,以1![]() 的速度沿
的速度沿![]() 向右运动,直到过点
向右运动,直到过点![]() 为止.在运动过程中,直线
为止.在运动过程中,直线![]() 始终垂直于
始终垂直于![]() ,若平移过程中直线
,若平移过程中直线![]() 扫过的面积为
扫过的面积为![]() (
(![]() ),直线
),直线![]() 的运动时间为
的运动时间为![]() ,则下列最能反映
,则下列最能反映![]() 与
与![]() 之间函数关系的图象是( )
之间函数关系的图象是( )
A.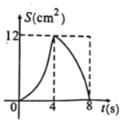 B.
B.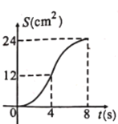
C.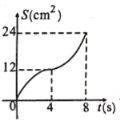 D.
D.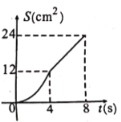
【答案】B
【解析】
连接![]() 交
交![]() 于点
于点![]() ,令直线
,令直线![]() 与
与![]() 或
或![]() 交于点
交于点![]() ,与
,与![]() 或
或![]() 交于点
交于点![]() ,则
,则![]() ,根据菱形
,根据菱形![]() 的周长为
的周长为![]() ,即可推出
,即可推出![]() ,根据勾股定理求出OD=OB,然后分情况讨论即可.
,根据勾股定理求出OD=OB,然后分情况讨论即可.
解:连接![]() 交
交![]() 于点
于点![]() ,令直线
,令直线![]() 与
与![]() 或
或![]() 交于点
交于点![]() ,与
,与![]() 或
或![]() 交于点
交于点![]() ,∵菱形
,∵菱形![]() 的周长为
的周长为![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
由勾股定理得![]() ,分两种情况:
,分两种情况:
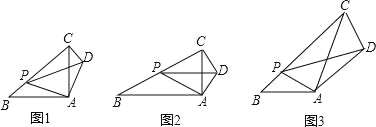
(1)当![]() 时,如图1,
时,如图1,
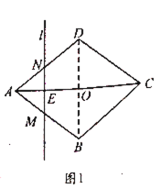
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
函数图象是开口向上,对称轴为![]() 轴且位于对称轴右侧的抛物线的一部分;
轴且位于对称轴右侧的抛物线的一部分;
(2)当![]() 时,如图2,
时,如图2,
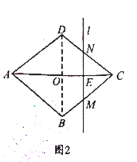
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
函数图象是开口向下,对称轴为直线![]() 且位于对称轴左侧的抛物线的一部分;
且位于对称轴左侧的抛物线的一部分;
故选B.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
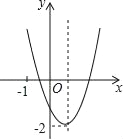
【题目】二次函数![]() (
(![]() ,
,![]() 是常数)中,自变量
是常数)中,自变量![]() 与函数
与函数![]() 的对应值如下表:
的对应值如下表:
| -1 |
| 0 |
| 1 |
| 2 |
| 3 |
|
|
| 1 |
| 2 |
| 1 |
| -2 |
(1)判断二次函数图象的开口方向,并写出它的顶点坐标;
(2)一元二次方程![]() (
(![]() ,
,![]() 是常数)的两个根
是常数)的两个根![]() ,
,![]() 的取值范围是下列选项中的哪一个 .
的取值范围是下列选项中的哪一个 .
A.![]() B.
B.![]()
C. ![]() D.
D.![]()