题目内容
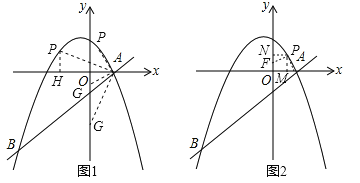
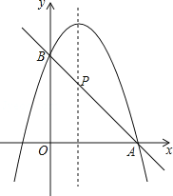
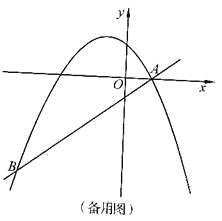
【题目】如图,在平面直角坐标系中,直线![]() 与抛物线
与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
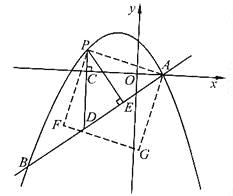
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
【答案】(1)![]() (2)①
(2)① ![]()
![]()
②满足题意的点P有三个,分别是![]()
![]()
【解析】
(1)利用直线解析式求出点A、B的坐标,再利用待定系数法求二次函数解析式解答;
(2)①利用直线解析式和抛物线解析式表示出PD,再利用同角的余角相等求出∠DPE=∠BAO,根据直线k值求出∠BAO的正弦和余弦值,然后表示出PE、DE,再根据三角形的周长公式列式整理即可得解,再根据二次函数的最值问题解答;
②分(i)点G在y轴上时,过点P作PH⊥x轴于H,根据正方形的性质可得AP=AG,∠PAG=90°,再求出∠PAH=∠AGO,然后利用“角角边”证明△APH和△GAO全等,根据全等三角形对应边相等可得PH=AO=2,然后利用二次函数解析式求解即可;(ii)点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,根据正方形的性质可得AP=FP,∠APF=90°,再根据同角的余角相等求出∠APM=∠FPN,然后利用“角边角”证明△APM和△FPN全等,根据全等三角形对应边相等可得PM=PN,从而得到点P的横坐标与纵坐标相等,再根据二次函数的解析式求解即可.
解:(1)令![]() ,则
,则![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,∴点A(2,0),B(﹣8,
,∴点A(2,0),B(﹣8,![]() ),把点A、B代入抛物线得,
),把点A、B代入抛物线得,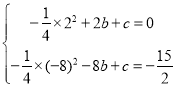 ,解得:
,解得: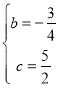 ,所以,该抛物线的解析式
,所以,该抛物线的解析式![]() ;
;
(2)①∵点P在抛物线上,点D在直线上,∴PD=![]() ,∵PE⊥AB,∴∠DPE+∠PDE=90°,又∵PD⊥x轴,∴∠BAO+∠PDE=90°,∴∠DPE=∠BAO,∵直线解析式
,∵PE⊥AB,∴∠DPE+∠PDE=90°,又∵PD⊥x轴,∴∠BAO+∠PDE=90°,∴∠DPE=∠BAO,∵直线解析式![]() ,∴sin∠BAO=
,∴sin∠BAO=![]() ,cos∠BAO=
,cos∠BAO=![]() ,∴PE=PDcos∠DPE=
,∴PE=PDcos∠DPE=![]() PD,DE=PDsin∠DPE=
PD,DE=PDsin∠DPE=![]() PD,∴△PDE的周长为l=PD+
PD,∴△PDE的周长为l=PD+![]() PD+
PD+![]() PD=
PD=![]() PD=
PD=![]() =
=![]() ,即
,即![]() ;∵
;∵![]() ,∴当x=﹣3时,最大值为15;
,∴当x=﹣3时,最大值为15;
②∵点A(2,0),∴AO=2,
分(i)点G在y轴上时,过点P作PH⊥x轴于H,在正方形APFG中,AP=AG,∠PAG=90°,∵∠PAH+∠OAG=90°,∠AGO+∠OAG=90°,∴∠PAH=∠AGO,在△APH和△GAO中,∵∠PAH=∠AGO,∠AHP=∠GOA=90°,AP=AG,∴△APH≌△GAO(AAS),∴PH=AO=2,∴点P的纵坐标为2,∴![]() ,整理得,
,整理得,![]() ,解得
,解得![]() ,∴点P(
,∴点P(![]() ,2)或P(
,2)或P(![]() ,2);
,2);
(ii)点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,在正方形APFG中,AP=FP,∠APF=90°,∵∠APM+∠MPF=90°,∠FPN+∠MPF=90°,∴∠APM=∠FPN,在△APM和△FPN中,∵∠APM=∠FPN,∠AMP=∠FNP=90°,AP=AF,∴△APM≌△FPN(AAS),∴PM=PN,∴点P的横坐标与纵坐标相等,∴![]() ,整理得,
,整理得,![]() ,解得
,解得![]() ,
,![]() (舍去),∴点P(
(舍去),∴点P(![]() ,
,![]() ).
).
综上所述,存在点P(![]() ,2)或P(
,2)或P(![]() ,2)或P(
,2)或P(![]() ,
,![]() ).
).