题目内容
【题目】如图，在平面直角坐标系中，点 A 和点 C 分别在x 轴和 y 轴的正半轴上，OA=6，OC=4，以 OA，OC 为邻边作矩形 OABC， 动点 M，N 以每秒 1 个单位长度的速度分别从点 A、C 同时出发，其中点 M 沿 AO 向终点 O 运动，点 N沿 CB 向终点 B 运动，当两个动点运动了 t 秒时，过点 N 作NP⊥BC，交 OB 于点 P，连接 MP．
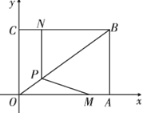
（1）直接写出点 B 的坐标为 ，直线 OB 的函数表达式为 ;
（2）记△OMP 的面积为 S，求 S 与 t 的函数关系式
；并求 t 为何值时，S有最大值，并求出最大值．
【答案】（1）
，
；（2）
，3，3．
【解析】
（1）根据四边形OABC为矩形即可求出点B坐标，设直线OB解析式为
，将B代入即可求直线OB的解析式；
（2）由题意可得
，由（1）可得点
的坐标为
， 表达出△OMP的面积即可，利用二次函数的性质求出最大值．
解：（1）∵OA=6，OC=4， 四边形OABC为矩形，
∴AB=OC=4，
∴点B，
设直线OB解析式为，将B代入得
，解得
，
∴，
故答案为：；
（2）由题可知，
，
由(1)可知，点的坐标为
，
∴当
时，
有最大值3．
练习册系列答案
相关题目
