题目内容
【题目】如图,已知直线y=﹣![]() x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ;点B的坐标为 ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)直线BC上是否存在一点M,使得△ABM的面积与△ABO的面积相等?若存在,请直接写出点M的坐标;若不存在,请说明理由.

【答案】(1)(4,0),(0,3);(2)y=﹣![]() x+3;(3)见解析.
x+3;(3)见解析.
【解析】
(1)利用待定系数法即可解决问题;
(2)设OC=x,则AC=BC=4﹣x,在Rt△BOC中,利用勾股定理求出x,再利用待定系数法求出直线BC的解析式即可;
(3)过点O作OM∥AB交直线BC于M.由OM∥AB,可知S△AOB=S△ABM,由直线AB的解析式为![]() ,OM∥AB,推出直线OM的解析式为
,OM∥AB,推出直线OM的解析式为![]() ,由
,由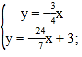 解得
解得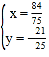 ,可得M
,可得M![]() ,根据对称性可知,经过点O′(0,6)与直线AB平行的直线与直线BC的交点M′,也满足条件.
,根据对称性可知,经过点O′(0,6)与直线AB平行的直线与直线BC的交点M′,也满足条件.
解:(1)令y=0,则x=4;令x=0,则y=3,
故点A的坐标为(4,0),点B的坐标为(0,3).
故答案为(4,0),(0,3);
(2)设OC=x,
∵直线CD垂直平分线段AB,
∴AC=CB=4﹣x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
32+x2=(4﹣x)2,
解得![]()
∴![]()
∴![]() 设直线BC的解析式为y=kx+b,
设直线BC的解析式为y=kx+b,
则有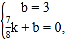
解得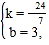
∴直线BC的解析式为![]()
(3)过点O作OM∥AB交直线BC于M.
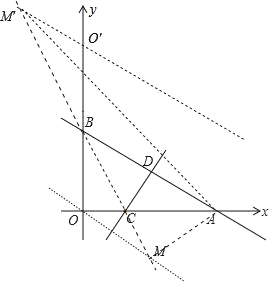
∵OM∥AB,
∴S△AOB=S△ABM,
∵直线AB的解析式为![]() ,OM∥AB,
,OM∥AB,
∴直线OM的解析式为![]()
由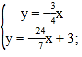 解得
解得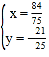 ,
,
∴M![]() ,
,
根据对称性可知,经过点O′(0,6)与直线AB平行的直线与直线BC的交点M′,也满足条件,易知BM′=BM,
设M′(m,n),则有![]()
∴![]()
∴M′![]()
综上所述,满足条件的点M坐标为![]() 或
或![]() .
.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案



