Question

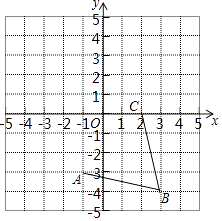
【题目】如图,在平面直角坐标系中,反比例函数y=kx-1（x＞0）的图象经过点A（1,2）和点B（m,n）（m＞1）,过点B作y轴的垂线，垂足为C．

（1）求该反比例函数解析式；

（2）当△ABC面积为2时,求点B的坐标．

（3）P为线段AB上一动点（P不与A、B重合）,在（2）的情况下,直线y=ax﹣1与线段AB交于点P，直接写出a的取值范围．

Answer 1

【答案】（1）y=（2）点B的坐标为（3， ）（3）＜a＜3．

【解析】试题分析：（1）根据待定系数法直接代入求解即可；

（2）利用代入法直接可得到m、n的关系，然后根据三角形的面积表示出m、n即可得到B的坐标；

（3）通过代入法求出a的两个值，然后根据动点确定a的范围.

试题解析：（1）∵反比例函数y=的图象经过点A（1，2），

∴k=1×2=2，∴反比例函数解析式为y=．

（2）∵点B（m，n）在反比例函数y=的图象上，∴mn=2．

又∵S△ABC=0.5BC（yA﹣yB）=0.5m（2﹣n）=m﹣0.5mn=m﹣1=2，

∴m=3，n=，∴点B的坐标为（3， ）．

（3）将A（1，2）代入y=ax﹣1中，2=a﹣1，解得：a=3；

将B（3， ）代入y=ax﹣1中， =3a﹣1，解得：a=．

∵直线y=ax﹣1与线段AB交于点P，P为线段AB上一动点（P不与A、B重合），

∴＜a＜3．