Question

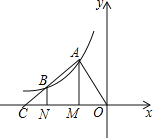
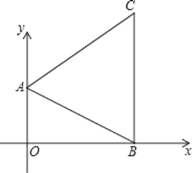
【题目】如图在直角坐标系中，已知A（0，a），B（b，0）C（3，c）三点，若a，b，c满足关系式：|a﹣2|+（b﹣3）2+＝0．

（1）求a，b，c的值．

（2）求四边形AOBC的面积．

（3）是否存在点P（x，﹣ x），使△AOP的面积为四边形AOBC的面积的两倍？若存在，求出点P的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）a＝2，b＝3，c＝4；（2）9；（3）存在点P（18，﹣9）或（﹣18，9），使△AOP的面积为四边形AOBC的面积的两倍．

【解析】

（1）根据“几个非负数相加和为0，则每一个非负数的值均为0”解出a，b，c的值；

（2）由点A、O、B、C的坐标可得四边形AOBC为直角梯形，根据直角梯形的面积公式计算即可；

（3）设存在点P（x，﹣ x），使△AOP的面积为四边形AOBC的面积的两倍．根据面积列出方程×2×|x|＝|x|＝2×9，解方程即可．

解：（1）∵|a﹣2|+（b﹣3）2+＝0，

∴a﹣2＝0，b﹣3＝0，c﹣4＝0，

∴a＝2，b＝3，c＝4；

（2）∵A（0，2），O（0，0），B（3，0），C（3，4）；

∴四边形AOBC为直角梯形，且OA＝2，BC＝4，OB＝3，

∴四边形AOBC的面积＝×（OA+BC）×OB＝×（2+4）×3＝9；

（3）设存在点P（x，﹣ x），使△AOP的面积为四边形AOBC的面积的两倍．

∵△AOP的面积＝×2×|x|＝|x|，

∴|x|＝2×9，

∴x＝±18

∴存在点P（18，﹣9）或（﹣18，9），

使△AOP的面积为四边形AOBC的面积的两倍．

故答案为：（1）a＝2，b＝3，c＝4；（2）9；（3）存在点P（18，﹣9）或（﹣18，9），使△AOP的面积为四边形AOBC的面积的两倍．