题目内容
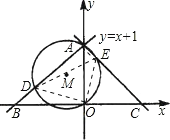
【题目】(12分)如图末-10,在平面直角坐标系中,直线y=x+1与y轴交于点A,与x轴交于点B,点C和点B关于y轴对称.
(1)求△ABC内切圆的半径;
(2)过O、A两点作⊙M,分别交直线AB、AC于点D、E,求证:AD+AE是定值,并求其值.

【答案】(1)![]() -1;(2)
-1;(2)![]()
【解析】试题分析:(1)因为直线y=x+1与y轴交于点A,与x轴交于点B,点C和点B关于y轴对称,所以分别令![]() 即可求出点
即可求出点![]() 的坐标,由此即可求出OA=OB=OC=1,所以可判断
的坐标,由此即可求出OA=OB=OC=1,所以可判断![]() 为Rt△,
为Rt△, ![]() 所以
所以![]() 代入相关数据即可求出内切圆的半径
代入相关数据即可求出内切圆的半径![]() ;
;
(2)连接OD,OE,DE.AE,因为![]() 根据
根据![]() 的圆周角对的弦是直径可得DE为直径,所以
的圆周角对的弦是直径可得DE为直径,所以![]() 又因
又因![]() 利用同角的余角相等可得
利用同角的余角相等可得![]() 因为
因为![]() 且OA=OB.可得△AOE≌△BOD.故AE=BD.所以
且OA=OB.可得△AOE≌△BOD.故AE=BD.所以![]()
试题解析:(1)∵直线AB的解解析式为:y=x+1,
∴A(0,1),B(1,0),
∵点C和点B关于y轴对称,
∴点C(1,0),
∴OA=OB=OC=1,
∵△ABC为Rt△, ![]()
∴![]() ,即内切圆的半径为
,即内切圆的半径为![]()
(2)连接OD,OE,DE.AE,
∵![]()
∴DE为直径.∴![]()
又∵![]()
又∵![]() 且OA=OB.
且OA=OB.
∴△AOE≌△BOD.故AE=BD.
∴![]()

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目