题目内容
【题目】如图,在△ABC中,AC=BC=2,∠A=∠B=30°,点D在线段AB上运动(点D不与A、B重合),连接CD,作∠CDE=30°,DE交BC于点E.
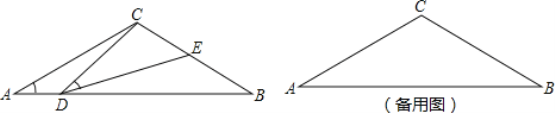
(1)AB=;
(2)当AD等于多少时,△ADC≌△BED,请说明理由;
(3)在点D的运动过程中,△CDE的形状可以是等腰三角形吗?若可以,求出AD的长;若不可以,说明理由.
【答案】(1)2![]() ;(2)当AD等于2
;(2)当AD等于2![]() -2时,△ADC≌△BED,理由见解析;(3)△CDE可以是等腰三角形,此时AD的长为2
-2时,△ADC≌△BED,理由见解析;(3)△CDE可以是等腰三角形,此时AD的长为2![]() -2或
-2或![]() .
.
【解析】
(1)过C作CM⊥AB于M,求出CM,根据勾股定理求出AM,代入AB=2AM求出即可.
(2)根据全等三角形的性质和判定得出BD=AC,求出BD,即可求出答案.
(3)分类讨论:当CD=DE时;当DE=CE时;当EC=CD时;然后利用等腰三角形的性质结合三角形内角和定理求出∠ADC或∠ACD的度数,继而根据勾股定理进行求解即可得.
(1)过C作CM⊥AB于M,
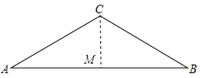
∵AC=BC,
∴AB=2AM,∠AMC=90°,
∵AC=2,∠A=30°,
∴CM=![]() AC=1,
AC=1,
由勾股定理得:AM=![]() ,
,
∴AB=2AM=2![]() ,
,
故答案为:2![]() ;
;
(2)当AD等于2![]() -2时,△ADC≌△BED,
-2时,△ADC≌△BED,
理由是:∵∠A=∠CDE=∠B=30°,
∴∠ACD+∠ADC=150°,∠ADC+∠EDB=150°,
∴∠ACD=∠EDB,
∴当AC=BD时,△ADC≌△BED,
即BD=AC=2,
∴AD=AB-BD=2![]() -2,
-2,
即得AD=2![]() -2时,△ADC≌△BED;
-2时,△ADC≌△BED;
(3)△CDE可以是等腰三角形,
∵△CDE是等腰三角形,
①如图1,当CD=DE时,
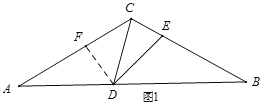
∵∠CDE=30°,
∴∠DCE=∠DEC=75°,
∴∠ADC=∠B+∠DCE=105°,
过点D作DF⊥AC,垂足为F,则∠AFD=∠CFD=90°
∵∠A=30°,
∴∠ADF=60°,AD=2DF,
∴∠CDF=45°,
∴∠FCD=45°=∠FDC,
∴CF=DF,
在Rt△ADF中,AF=![]() ,
,
∵AF+CF=AC=2,
∴![]() DF+DF=2,
DF+DF=2,
∴DF=![]() ,
,
∴AD=2![]() -2;
-2;
②如图2,当DE=CE时,
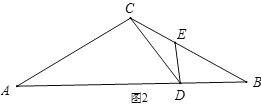
∵∠CDE=30°,
∴∠DCE=∠CDE=30°,
∴∠ACD=120°-30°=90°,
∵∠A=30°,
∴CD=![]() AD,
AD,
在Rt△ACD中,AD2=AC2+CD2,
即AD2=22+(![]() AD)2,
AD)2,
∴AD=![]() ;
;
③当EC=CD时,
∠BCD=180°-∠CED-∠CDE=180°-30°-30°=120°,
∵∠ACB=180°-∠A-∠B=120°,
∴此时,点D与点A重合,不合题意,
综上,△ADC可以是等腰三角形,此时AD的长为2![]() -2或AD=
-2或AD=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】小红爸爸上星期五买进某公司股票1000股,每股28元,下表为本周内每日该股票的涨跌情况。(单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 |
(1)通过上表你认为星期三收盘时,每股是多少?
(2)本周内每股最高是多少?最低是多少元?
(3)已知小红爸爸买进股票时付了![]() 的手续费,卖出时还需付成交额,
的手续费,卖出时还需付成交额,![]() 的手续费和
的手续费和![]() 的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?
的交易税,如果小红爸爸在星期五收盘时将全部股票卖出,你对他的收益情况怎样评价?