Question

【题目】如图，在平行四边形ABCD中，E，F分别是AB，CD的中点，AF与DE相交于点G，BF与CE相交于点H．

（1）求证：四边形EHFG是平行四边形；

（2）①若四边形EHFG是菱形，则平行四边形ABCD必须满足条件　 　；

②若四边形EHFG是矩形，则平行四边形ABCD必须满足条件　 　．

Answer 1

【答案】（1）证明见解析；（2）①平行四边形ABCD是矩形；②当平行四边形ABCD是矩形，并且AB=2AD．

【解析】

（1）通过证明两组对边分别平行，可得四边形EHFG是平行四边形；
（2）①当平行四边形ABCD是矩形时，通过证明有一组邻边相等，可得平行四边形EHFG是菱形；
②当平行四边形ABCD是矩形，并且AB=2AD时，先证明四边形ADFE是正方形，得出有一个内角等于90°，从而证明菱形EHFG为一个矩形

（1）证明：∵四边形ABCD是平行四边形，

∴AE∥CF，AB=CD，

∵E是AB中点，F是CD中点，

∴AE=CF，

∴四边形AECF是平行四边形，

∴AF∥CE．

同理可得DE∥BF，

∴四边形FGEH是平行四边形；

（2）①当平行四边形ABCD是矩形时，平行四边形EHFG是菱形．

∵四边形ABCD是矩形

∴∠ABC=∠DCB=90°，

∵E是AB中点，F是CD中点，

∴BE=CF，

在△EBC与△FCB中，

∵ ，

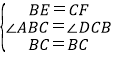∴△EBC≌△FCB，

∴CE=BF，

∠ECB=∠FBC，

BH=CH，

EH=FH，

平行四边形EHFG是菱形；

②解：当平行四边形ABCD是矩形，并且AB=2AD时，平行四边形EHFG是矩形．理由如下：

连接EF，如图所示：

∵E，F分别为AB，CD的中点，且AB=CD，

∴AE=DF，且AE∥DF，

∴四边形AEFD为平行四边形，

∴AD=EF，

又∵AB=2AD，E为AB中点，则AB=2AE，

于是有AE=AD=AB，

这时，EF=AE=AD=DF=AB，∠EAD=∠FDA=90°，

∴四边形ADFE是正方形，

∴EG=FG=AF，AF⊥DE，∠EGF=90°，

∴此时，平行四边形EHFG是矩形；

故答案为：当平行四边形ABCD是矩形，平行四边形ABCD是矩形，并且AB=2AD．