题目内容
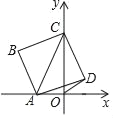
【题目】如图,点A是x轴负半轴上的一个动点,点C在y轴上,以AC为对角线画正方形ABCD,已知点C的坐标是C(0,4),设点A的坐标为A(n,0),连接OD,当OD=![]() 时,n=_____.
时,n=_____.
【答案】-2
【解析】
先求得OD与y轴的夹角为45°,然后依据OD的长,可求得OF和DF的长,作辅助线,构建全等三角形,再证明△AFD≌△DEC,从而可得到AF=DE=3,从而可得到点A的坐标.
解:如图所示:过点D作EF⊥x轴于F,过C作CE⊥EF于E,
∵四边形ABCD为正方形,
∴A、B、C、D四点共圆,∠DAC=45°.
又∵∠COA=90°,
∴点O也在这个圆上,
∴∠COD=∠CAD=45°.
又∵OD=![]() ,
,
∴OF=DF=1.
∵C(0,4),
∴OC=EF=4,
∴DE=4﹣1=3,
∵四边形ABCD为正方形,
∴AD=CD,
∵∠ADC=90°,
∴∠ADF+∠CDE=∠CDE+∠DCE=90°,
∴∠ADF=∠DCE,
∵∠AFD=∠DEC=90°,
∴△AFD≌△DEC(SAS),
∴AF=DE=3,
∴AO=2,
∴A(﹣2,0),即n=﹣2;
故答案为:﹣2.

【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.