题目内容
【题目】如图,点A是反比例函数y=![]() (x>0)图象上一点,直线y=kx+b过点A并且与两坐标轴分别交于点B,C,过点A作AD⊥x轴,垂足为D,连接DC,若△BOC的面积是4,则△DOC的面积是______.
(x>0)图象上一点,直线y=kx+b过点A并且与两坐标轴分别交于点B,C,过点A作AD⊥x轴,垂足为D,连接DC,若△BOC的面积是4,则△DOC的面积是______.

【答案】2![]() ﹣2.
﹣2.
【解析】
先用三角形BOC的面积得出k=![]() ①,再判断出△BOC∽△BDA,得出a2k+ab=4②,联立①②求出ab,即可得出结论.
①,再判断出△BOC∽△BDA,得出a2k+ab=4②,联立①②求出ab,即可得出结论.
设A(a,![]() )(a>0),
)(a>0),
∴AD=![]() ,OD=a,
,OD=a,
∵直线y=kx+b过点A并且与两坐标轴分别交于点B,C,
∴C(0,b),B(﹣![]() ,0),
,0),
∵△BOC的面积是4,
∴S△BOC=![]() OB×OC=
OB×OC=![]() ×
×![]() ×b=4,
×b=4,
∴b2=8k,
∴k=![]() ①
①
∴AD⊥x轴,
∴OC∥AD,
∴△BOC∽△BDA,
∴![]() ,
,
∴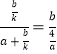 ,
,
∴a2k+ab=4②,
联立①②得,ab=﹣4﹣4![]() (舍)或ab=4
(舍)或ab=4![]() ﹣4,
﹣4,
∴S△DOC=![]() ODOC=
ODOC=![]() ab=2
ab=2![]() ﹣2.
﹣2.
故答案为:2![]() ﹣2.
﹣2.

练习册系列答案
相关题目







