题目内容
【题目】已知，如图，ABCD中，BC=8cm，CD=4cm，∠B=60°，点M从点D出发，沿DA方向匀速运动，速度为2cm/s，点N从点B出发，沿BC方向匀速运动，速度为1cm/s，过M作MF⊥CD，垂足为F，延长FM交BA的延长线于点E，连接EN，交AD于点O，设运动时间为t（s）（0＜t＜4），解答下列问题：
（1）当t为何值时，△AEM≌△DFM？
（2）连接AN，MN，设四边形ANME的面积为y（cm2），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使四边形ANME的面积是ABCD面积的 
？若存在，求出相应的t值，若不存在，说明理由；
（4）连接AC，交EN于点P，当EN⊥AD时，求线段OP的长度．
【答案】
（1）
解：∵四边形ABCD为平行四边形，
∴AD=BC=8．
∵△AEM≌△DFM，
∴AM=MD=4．
∴2t=4．
∴t=2
（2）
解：如图1所示：过点A作AG⊥BC，垂足为G．
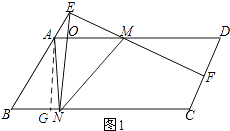
∵∠AGB=90°，∠A=60°，
∴AG= 
AB=2 
∵MD=2t，
∴AM=8﹣2t．
∵AB∥CD，MF⊥CD，
∴MF⊥AB．
∴∠MEA=90°．
∵AD∥BC，
∴∠EAM=∠B=60°．
∴AE= 
AM=4﹣t，ME= （4﹣t）．
∴y=S△ANM+S△AEM= ×（8﹣2t）×2 + ×（4﹣t）× ×（4﹣t）= t2﹣6 t+16 ．
∴y= t2﹣6 t+16
（3）
解：设运动时间t秒时，四边形ANME的面积是ABCD面积的 
．
根据题意得： t2﹣6 t+16 = ×8×2 ．
整理得：t2﹣12t+11=0．
解得t=1或t=11（舍去）．
所以当t=1时，四边形ANME的面积是ABCD面积的
（4）
解：如图2所示：过A作AG⊥BC，垂足为G．
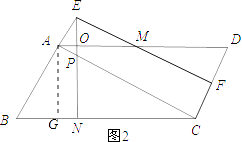
∵由（2）可知AE=4﹣t．
∴BE=AB+AE=8﹣t．
∵∠B=60°，EN⊥BC，AG⊥BC，
p>∴BN= BE=4﹣ t，BG= AB=2．又∵BN=t，
∴4﹣ t=t．
解得：t= 
．
∴GN=BN﹣BG= 
．
∴AO= ，NC= 
．
设PO=x，则PN=2 ﹣x．
∵AO∥NC，
∴△AOP∽△CNP．
∴ 
，即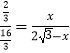 
．
解得：x= 
．
∴OP的长为
【解析】（1）由全等三角形的性质可知AM=MD=4，故此得到2t=4，于是可求得t的值；（2）过点A作AG⊥BC，垂足为G．在Rt△ABG中依据特殊锐角三角函数值可求得AG的长，由题意可得到AM=8﹣2t，然后再△AEM中依据特殊锐角三角函数值可求得AE、ME的长，最后依据y=S△ANM+S△AEM可得到y与x的函数关系式；（3）设运动时间t秒时，四边形ANME的面积是ABCD面积的 ，根据题意列方程求解即可；（4）过A作AG⊥BC，垂足为G．由（2）可知AE=4﹣t，从而得到BE的长，然后在△AGB和△BNE中，依据特殊锐角三角函数值可求得NB的长（含t的式子），接下来依据BN=t列出关于t的方程，从而可求得t的值，于是可求得AO、NC的长，最后证明△AOP∽△CNP，最后依据相似三角形的性质可求得OP的长．
