题目内容
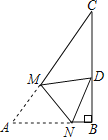
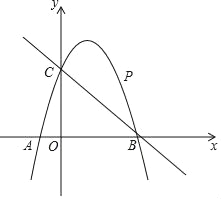
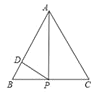
【题目】如图,正△ABC中,点P为BC边上的任意一点(不与点B,C重合),且∠APD= 60° ,PD交边AB于点D. 设BP= x ,BD= y ,右图为y关于x的函数大致图象,下列判断中正确的是( )
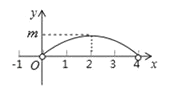
①正△ABC中边长为4;②图象的函数表达式是![]() , 其中 0<x<4;③ m=1
, 其中 0<x<4;③ m=1
A. ①②③B. ①②C. ②③D. ①③
【答案】D
【解析】
设正△ABC边长为a,根据等边三角形性质可知∠B=∠C=60°,由三角形内角和定理和平角性质得∠CAP+∠APC=120°,∠BPD+∠APC=120°,等量代换可得∠CAP=∠BPD,根据相似三角形判定和性质得CA:BP=CP:BD,代入数值可得y关于x的函数解析式为:![]() ;由二次函数性质和图像可得x=
;由二次函数性质和图像可得x=![]() =2,从而可得a值,即正△ABC边长为4,故①正确;将a值代入可得y关于x的函数解析式为
=2,从而可得a值,即正△ABC边长为4,故①正确;将a值代入可得y关于x的函数解析式为![]() ,故②错误;将二次函数解析式配方得
,故②错误;将二次函数解析式配方得![]() ,从而可得
,从而可得
m=1,故③正确.
解:∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵∠APD=60°,
∴∠CAP+∠APC=120°,∠BPD+∠APC=120°,
∴∠CAP=∠BPD,
∴△CAP∽△BPD,
∴CA:BP=CP:BD,
设正△ABC边长为a,
∴CA=CB=a,CP=CB-BP=a-x,
∵ BP= x ,BD= y ,
∴a:x=(a-x):y,
即![]() ,
,
∴ y关于x的函数解析式为:![]() ,
,
∵抛物线对称轴为:x=![]() =2,
=2,
∴a=4,
∴正△ABC边长为4,
故①正确;
∴y关于x的函数解析式为:![]() ,
,
故②错误;
∵![]() ,
,
∴m=1,
故③正确;
综上所述:正确的有①③.
故答案为:D.

练习册系列答案
相关题目