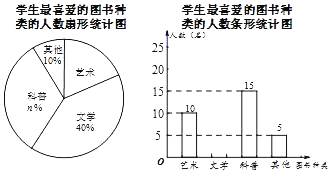
题目内容
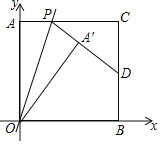
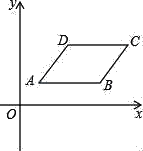
【题目】如图,在平面直角坐标系中,ABCD的边AB=2,顶点A坐标为(1,b),点D坐标为(2,b+1)
(1)点B的坐标是 ,点C的坐标是 (用b表示);
(2)若双曲线y=![]() 过ABCD的顶点B和D,求该双曲线的表达式;
过ABCD的顶点B和D,求该双曲线的表达式;
(3)若ABCD与双曲线y=![]() (x>0)总有公共点,求b的取值范围.
(x>0)总有公共点,求b的取值范围.
【答案】(1)(3,b);(4,b+1);(2)y=![]() ;(3)0≤b≤4.
;(3)0≤b≤4.
【解析】
(1)由四边形ABCD为平行四边形,得到A与B纵坐标相同,C与D纵坐标相同,横坐标相差2,得出B、C坐标即可;
(2)根据B与D在反比例图象上,得到C与D横纵坐标乘积相等,求出b的值确定出B坐标,进而求出k的值,确定出双曲线解析式;
(3)抓住两个关键点,将A坐标代入双曲线解析式求出b的值;将C坐标代入双曲线解析式求出b的值,即可确定出平行四边形与双曲线总有公共点时b的范围.
解:(1)根据题意得:B(3,b),C(4,b+1).
故答案为:B(3,b),C(4,b+1);
(2)∵双曲线y=![]() 过点B(3,b)和D(2,b+1),
过点B(3,b)和D(2,b+1),
∴3b=2(b+1),
解得b=2,
∴B点坐标为(3,2),D点坐标(2,3),
把B点坐标(3,2)代入y=![]() ,解得k=6;
,解得k=6;
∴双曲线表达式为y=![]() ;
;
(3)∵ABCD与双曲线y=![]() (x>0)总有公共点,
(x>0)总有公共点,
∴当点A(1,b)在双曲线y=![]() ,得到b=4,
,得到b=4,
当点C(4,b+1)在双曲线y=![]() ,得到b=0,
,得到b=0,
∴b的取值范围0≤b≤4.

练习册系列答案
相关题目