题目内容
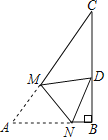
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
【答案】![]() 或
或![]()
【解析】依据△DCM为直角三角形,需要分两种情况进行讨论:当∠CDM=90°时,△CDM是直角三角形;当∠CMD=90°时,△CDM是直角三角形,分别依据含30°角的直角三角形的性质以及等腰直角三角形的性质,即可得到折痕MN的长.
分两种情况:
①如图,当∠CDM=90°时,△CDM是直角三角形,
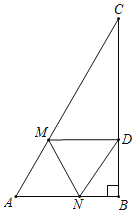
∵在Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,
+4,
∴∠C=30°,AB=![]() AC=
AC=![]() +2,
+2,
由折叠可得,∠MDN=∠A=60°,
∴∠BDN=30°,
∴BN=![]() DN=
DN=![]() AN,
AN,
∴BN=![]() AB=
AB=![]() ,
,
∴AN=2BN=![]() ,
,
∵∠DNB=60°,
∴∠ANM=∠DNM=60°,
∴∠AMN=60°,
∴AN=MN=![]() ;
;
②如图,当∠CMD=90°时,△CDM是直角三角形,
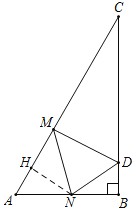
由题可得,∠CDM=60°,∠A=∠MDN=60°,
∴∠BDN=60°,∠BND=30°,
∴BD=![]() DN=
DN=![]() AN,BN=
AN,BN=![]() BD,
BD,
又∵AB=![]() +2,
+2,
∴AN=2,BN=![]() ,
,
过N作NH⊥AM于H,则∠ANH=30°,
∴AH=![]() AN=1,HN=
AN=1,HN=![]() ,
,
由折叠可得,∠AMN=∠DMN=45°,
∴△MNH是等腰直角三角形,
∴HM=HN=![]() ,
,
∴MN=![]() ,
,
故答案为:![]() 或
或![]() .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案【题目】甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | 第九次 | 第十次 | |
甲 | 7 | 10 | 8 | 10 | 9 | 9 | 10 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 9 | 9 | 10 | 8 | 10 | 7 | 10 |
(1)选手甲的成绩的中位数是 分;选手乙的成绩的众数是 分;
(2)计算选手甲的平均成绩和方差;
(3)已知选手乙的成绩的方差是15,则成绩较稳定的是哪位选手?请直接写出结果.