题目内容
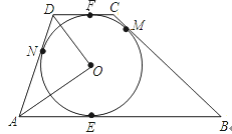
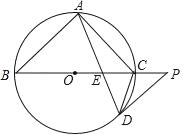
【题目】如图,已知BC是⊙O的直径,点A,D在⊙O上,∠B=2∠CAD,在BC的延长线上有一点P,使得∠P=∠ACB,弦AD交直径BC于点E.
(1)求证:DP与⊙O相切;
(2)判断△DCE的形状,并证明你的结论;
(3)若CE=2,DE=![]() ,求线段BC的长度.
,求线段BC的长度.
【答案】(1)证明见解析;(2)△DCE是等腰三角形,证明见解析;(3)10.
【解析】
(1)连接OD,根据圆周角定理得到∠DOP=2∠DAC,等量代换得到∠COD=∠B,根据圆周角定理得到∠BAC=90°,根据切线的判定定理即可得到结论;
(2)根据圆周角定理和三角形的内角和即可得到结论;
(3)根据相似三角形的性质得到![]() ,于是得到OC=
,于是得到OC=![]() =5,即可得到结论.
=5,即可得到结论.
(1)连接OD,

∴∠DOP=2∠DAC,
∵∠B=2∠CAD,
∴∠COD=∠B,
∵∠P=∠ACB,
∴∠ODP=∠BAC,
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠ODP=90°,
∴DP与⊙O相切;
(2)△DCE是等腰三角形,
理由:∵∠B=∠COD,∠BOD=180°﹣∠COD,∠BAD+∠AEB=180°﹣∠B,
∴∠BOD=∠BAD+∠AEB,
∵∠BAD=![]() ∠BOD,
∠BOD,
∴∠AEB=![]() ∠BOD,
∠BOD,
∴∠BAD=∠AEB,
∵∠DCE=∠BAE,∠CED=∠AEB,
∴∠CED=∠DCE,
∴△DCE是等腰三角形;
(3)∵OC=OD,
∴∠OCD=∠ODC,
∵DE=DC,
∴∠OCD=∠CED,
∴∠DEC=∠DCE=∠OCD=∠ODC,
∴△DCE∽△OCD,
∴![]() ,
,
∵CE=2,DE=![]() ,
,
∴CD=DE=![]() ,
,
∴OC=![]() =5,
=5,
∴BC=2OC=10.

练习册系列答案
相关题目