题目内容
【题目】阅读材料:
我们知道,![]() ,类似地,我们把
,类似地,我们把![]() 看成一个整体,则
看成一个整体,则![]()
![]() =
=![]() .“整体思想”是初中数学解题中的一种重要的思想方法,它在多项式的化简与求职中应用极为广泛.
.“整体思想”是初中数学解题中的一种重要的思想方法,它在多项式的化简与求职中应用极为广泛.
尝试应用:
(1)把![]() 看成一个整体,合并
看成一个整体,合并![]() 的结果为_______.
的结果为_______.
(2)已知![]() ,求
,求![]() 的值.
的值.
拓广探索:
(3)已知![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)-33;(3)732.
;(2)-33;(3)732.
【解析】
(1)利用整体思想,把(ab)2看成一个整体,合并3(ab)26(ab)2+2(ab)2即可得到结果;
(2)原式可化为3(x22y)21,把x22y=4整体代入即可;
(3)依据a2b=3,2bc=5,cd=10,即可得到ac=8,2bd=15,整体代入进行计算即可.
解:(1)(1)∵3(ab)26(ab)2+2(ab)2=(36+2)(ab)2=(ab)2;
(2)原式![]()
将![]() 代入,得
代入,得
原式=![]() .
.
(3)![]()
∴![]()
![]()
![]()
![]()
![]() .
.
故答案为:(1)![]() ;(2)-33;(3)732.
;(2)-33;(3)732.

练习册系列答案
相关题目
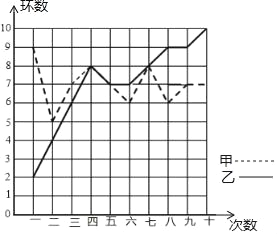
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.