题目内容
【题目】如图,在平行四边形ABCD中,E,F分别是AB,AD的中点,若△AEF的面积为5cm2,则平行四边形ABCD的面积是_____cm2.
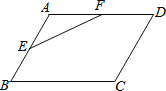
【答案】40
【解析】
连结BD,根据三角形中位线定理得出EF∥BD,EF=![]() BD,那么△AEF∽△ABD,利用相似三角形面积比等于相似比的平方求出S△ABD=4S△AEF=20cm2,根据平行四边形的性质得出AD∥BC,AD=BC,由等底等高的三角形面积相等得出S△CBD=S△ADB=20cm2,于是SABCD=40cm2.
BD,那么△AEF∽△ABD,利用相似三角形面积比等于相似比的平方求出S△ABD=4S△AEF=20cm2,根据平行四边形的性质得出AD∥BC,AD=BC,由等底等高的三角形面积相等得出S△CBD=S△ADB=20cm2,于是SABCD=40cm2.
解:如图,连结BD.
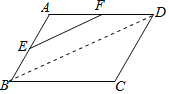
∵E、F分别是AB、AD的中点,
∴EF∥BD,EF=![]() BD,
BD,
∴△AEF∽△ABD,
∴![]() ,
,
∴S△ABD=4S△AEF=20cm2,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴S△CBD=S△ADB=20cm2,
∴SABCD=40cm2,
故答案为:40.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目