题目内容
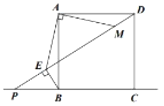
【题目】已知：如图，正方形ABCD，点P是直线BC上一个动点，连接PD交直线AB于点O，过点B作BE⊥PD于点E，连接AE．
（1）如图1，
①直接写出∠AED的度数；
②用等式表示线段AE、BE和DE之间的数量关系，并证明；
（2）当点P运动到图2和图3所示的位置时，请选择其中一种情况补全图形，并接写出线段AE、BE和DE之间的数量关系．
【答案】（1）①45° ②
，证明见解析 （2）作图见解析，
【解析】
（1）①如图1，过点A作
，交PD于M，通过证明
，可得
，即可求出
；②由①可得
，，
，从而得出
，即可得证；
（2）根据题意补全图形，同理通过证明
，即可得证．
（1）①如图1，过点A作，交PD于M
∵四边形ABCD是正方形
∴；
②
由①可得，，
；
（2）所画图形如图2、图3．
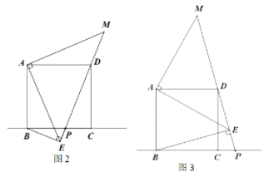
猜想：
同理可证
∴
练习册系列答案
相关题目
