题目内容
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() ,与
,与![]() 轴交于
轴交于![]() .
.
(1)若![]() ,求抛物线的解析式,并写出抛物线的对称轴;
,求抛物线的解析式,并写出抛物线的对称轴;
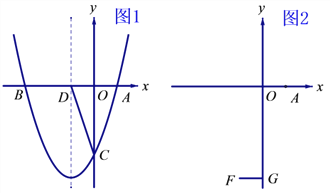
(2)如图1,在(1)的条件下,设抛物线的对称轴交轴于![]() ,在对称轴左侧的抛物线上有一点
,在对称轴左侧的抛物线上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,设![]() ,
, ![]() 于
于![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)抛物线的解析式为:y=x2+2x-3,对称轴为:x=-1;(2)点E坐标为(-4,5);(3)m的取值范围是:-4≤m≤4,且m≠0.
【解析】试题分析:(1)利用待定系数法即可得解析式,再根据抛物线对称轴公式即可得对称轴;
(2)先求出AC的解析式,然后求出过点D与AC平行的直线解析式,即可得到直线AC向上平移了6个单位长度,再根据![]() 可知点E为直线AC向上平移20个单位长度后与抛物线的交点,联立解析式解方程组即可得;
可知点E为直线AC向上平移20个单位长度后与抛物线的交点,联立解析式解方程组即可得;
(3)分m>0、m<0两种情况进行讨论即可得.
试题解析:(1)∵![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() ,m=-3,
,m=-3,
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为:y=x2+2x-3,
对称轴为:x=-1;
(2)∵点A(1,0),C(0,-3),
∴直线AC为y= 3x-3,
∴过点D(-1,0)且平行于AC的直线ll为:y= 3x+3,
∴直线AC向上平移6个单位得到直线l1,
∴将直线AC向上平移![]() 个单位得到直线l2:y=3x+17,
个单位得到直线l2:y=3x+17,
联立方程组, ![]() ,
,
解得, ![]() ,
, ![]() (不合题意,舍去),
(不合题意,舍去),
∴点E坐标为(-4,5);
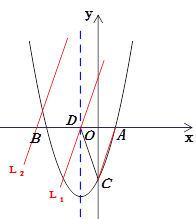
(3)设点P(0,y),
①当m<0时,如图所示,易证△POB~△FPG,得![]() ,
,
∴![]() ,
,
∴m=y2+4y=(y+2)2-4,
∵-4<y<0,
∴-4≤m<0;
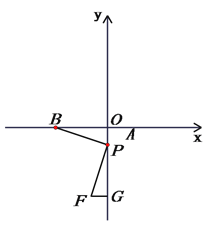
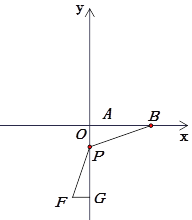
②当m>0时,如图所示,易证△POB~△FPG,得![]() ,
,
∴![]() ,
,
∴m= -y2 -4y= -(y+2)2+4,
∵-4<y<0,
∴0<m≤4,
综上所述,m的取值范围是:-4≤m≤4,且m≠0.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案







