题目内容
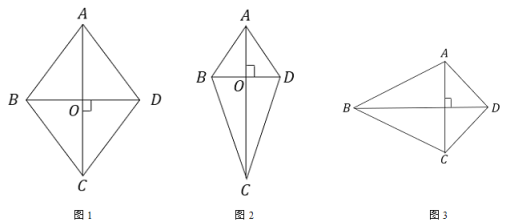
【题目】已知,在四边形ABCD中,AD∥BC,AB∥DC,点E在BC延长线上,连接DE,∠A+∠E=180°.
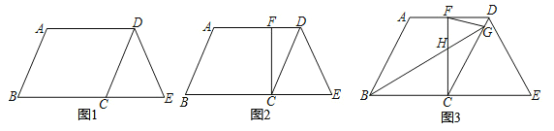
(1)如图1,求证:CD=DE;
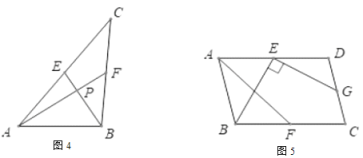
(2)如图2,过点C作BE的垂线,交AD于点F,请直接写出BE、AF、DF 之间的数量关系_______________________;
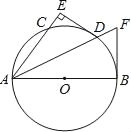
(3)如图3,在(2)的条件下,∠ABC的平分线,交CD于G,交CF于H,连接FG,若∠FGH=45°,DF=8,CH=9,求BE的长.
【答案】(1)证明见解析;(2)BE=AF+3DF;(3)31
【解析】
(1)利用等角的补角判断出∠DCE=∠E即可;
(2)先判断出四边形CFDN是矩形,再判断出CN=NE=FD,即可得出结论;
(3)先判断出∠ABG=∠BGC,进而得出四边形BCFM是正方形,即可判断出△BMK≌△BCH,再用勾股定理求出BM=15,即可得出AD=BC=BM=15,即可求出结论.
(1)∵![]()
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
∴∠A=∠BCD,
∵∠A+∠E=180°,∠BCD+∠DCE=180°,
∴∠DCE=∠E,
∴CD=DE;
(2)如图2,过点D作DN⊥BE于N,
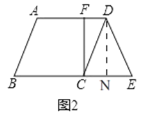
∵CF⊥BE,
∴∠DNC=∠BCF=90°,
∴FC∥DN,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴四边形CFDN是矩形,
∴FD=CN,
∵CD=DE,DN⊥CE,
∴CN=NE=FD,
∵四边形ABCD是平行四边形,
∴BC=AD=AF+FD,
∴BE=AF+3DF.
(3)如图3,过点B作BM⊥AD于点M,延长FM至K,使KM=HC.连接BK,
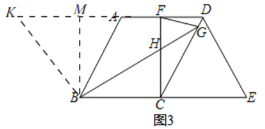
∵ABCD,
∴AB∥CD,
∴∠ABG=∠BGC,
∵BG平分∠ABC,
∴设∠ABG=∠CBG=∠BGC=α,
∴BC=CG,
∵∠FGH=45°,
∴∠FGC=45°+α,
∵∠BCF=90°,
∴∠BHC=∠FHG=90°-α,
∴∠HFG=45°+α=∠FGC,
∴FC=CG=BC,
∵BM⊥AD,
∴∠MBC=90°=∠FCE=∠MFC,
∴四边形BCFM是矩形,
∵BC=FC,
∴四边形BCFM是正方形,
∴BM=MF=BC=AD,
∴MA=DF=8,
∵∠KMB=∠BCH=90°,KM=CH,
∴△BMK≌△BCH,
∴KM=CH=9,∠KBM=∠CBH=α,∠K=∠BHC=90°-α,
∵∠MBC=90°,
∴∠MBA=90°-2α,
∴∠KBA=90°-α=∠K,
∴AB=AK=8+9=17,
在Rt△ABM中,∠BMA=90°,BM=![]() =15,
=15,
∴AD=BC=BM=15,
∴AF=AD-DF=15-8=7,
∴BE=AF+3DF=7+3×8=31.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |