题目内容
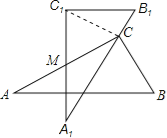
【题目】如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角尺ABC,使其直角顶点C恰好落在三角尺A′B′C′的斜边A′B′上.当∠A=30°,AC=10时,两直角顶点C,C′间的距离是_____.

【答案】5
【解析】试题分析:连接CC1,根据M是AC、A1C1的中点,AC=A1C1,得出CM=A1M=C1M=![]() AC=5,再根据∠A1=∠A1CM=30°,得出∠CMC1=60°,△MCC1为等边三角形,从而证出CC1=CM,即可得出答案.
AC=5,再根据∠A1=∠A1CM=30°,得出∠CMC1=60°,△MCC1为等边三角形,从而证出CC1=CM,即可得出答案.
解:如图,连接CC1,
∵两块三角板重叠在一起,较长直角边的中点为M,
∴M是AC、A1C1的中点,AC=A1C1,
∴CM=A1M=C1M=![]() AC=5,
AC=5,
∴∠A1=∠A1CM=30°,
∴∠CMC1=60°,
∴△CMC1为等边三角形,
∴CC1=CM=5,
∴CC1长为5.
故答案为5.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目