Question

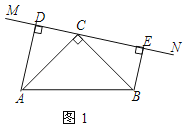
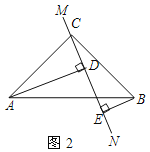
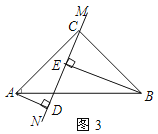
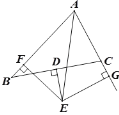
【题目】如图，在△ABC中，D为BC的中点，DE⊥BC交∠BAC 的平分线AE于E，EF⊥AB于F，EG⊥AC交AC延长线于G. AB=6, AC=3,求BF 的长.

Answer 1

【答案】1.5

【解析】

通过角平分线的性质可知EF=EG，再根据垂直平分线的性质，EC=EB，可得△BEF≌△CEG，再根据AB-BF=AC+CG,可以求得BF的值.

证明：连接EB、EC，

∵AE平分∠BAC，EF⊥AB，EG⊥AC，

∴EF=EG，

在Rt△AFE和Rt△AGE中，

∴Rt△AEF≌Rt△AEG（HL），

∴AF=AG

又∵D为BC中点，ED⊥BC，

∴EB=EC，

在Rt△BFE和Rt△CGE中，

∴Rt△BEF≌Rt△CEG（HL），

∴BF=CG．

∵AF=AG

∴AB-BF=AC+CG

∴AB-AC=2BF

∴BF=1.5